Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 53
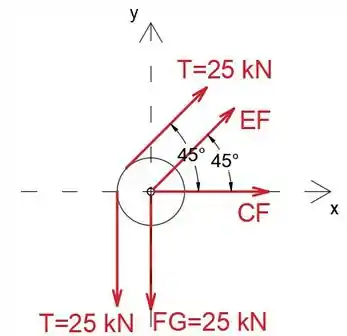
Determine as forças nos membros FG, CG, BC e EF para a treliça do guindaste carregado.
Passo 1
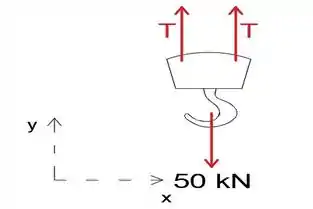
Primeiro, vamos isolar e desenhar o diagrama de corpo livre do gancho para determinar a tensão no cabo.
Equacionando a soma das forças na direção y a zero, podemos calcular a tensão T
Passo 2
Podemos passar uma seção diretamente pelos membros BC, CG e FG e analisar uma parte superior da treliça, porque não há apoios ou cortinas desconhecidas na seção certa
Vamos supor que todos os membros selecionados em tensão
Observe que todas as diagonais formam um ângulo de 45∘ com uma horizontal
Passo 3
Ao igualar a soma dos momentos sobre o ponto G a zero, eliminaremos as forças FG e CG, de modo que a única incógnita será BC
Como obtivemos o resultado negativo, isso significa que o membro está em compressão
Passo 4
Equacionando a soma das forças na direção x a zero, podemos determinar a força CG
Equacionando a soma das forças na direção y a zero, podemos determinar a força FG
Substitua BC por seu valor
Passo 5
Finalmente, podemos determinar a força no membro EF analisando a junta F
Observe que vamos supor que todos os membros desconhecidos estão em tensão
