Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 46
Determine a coordenada do centroide do volume gerado pela revolução da área sombreada do triangulo direito em torno do eixo por como mostrado na figura.
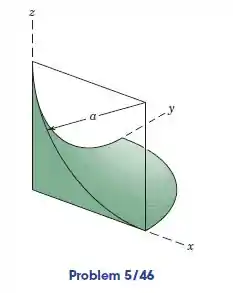
Passo 1
Oi pessoal? Vamos para mais um exercício?
O ângulo de fricção é dado por:
Substituindo o coeficiente de atrito, temos que:
Temos que:
Portanto:
Os dois ângulos agirão juntos em um eixo e um contra o outro no outro eixo. Portanto:
Resposta
Exercícios de Livros Relacionados
5.27. If the shaded area of Prob. 5/26 is rotated about the y-axis, determine the y-coordinate of the centroid of the resulting volume.
5.28. Determine the x- and y-coordinates of the centroid of the shaded area.
Localize o centroide y - do hemisfério.
Localize o centroide x - da área.
Localize o centroide y - da área.