Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas de Revisão - Ex. 2

Localize o centroide overset(-)(y) da área.

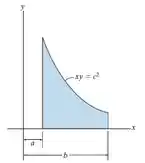
Passo 1

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Precisamos descobrir o centroide overset(-)(y) da área da figura.

Para isto, basta lembrarmos da seguinte relação:

overset(-)(y) = (int_A^() y d A)/(int_A^() d A)

Então, nós só precisamos desenvolver estas duas integrais e depois fazer a razão dos dois!

Sendo assim, vamos as contas!

Passo 2

Vamos começar trabalhando com a integral do numerador de overset(-)(y) .

Para isto, vamos analisar a nossa região como uma do tipo I (primeiro integramos em relação a y e depois em relação a x). Os limites de integração são: a <= x <= b e 0 <= y <= c^2 // x . Sendo assim, temos:

int_A^() y d A = int_a^b int_0^(c^2 // x) y d y d x

int_a^b ((y^2)/(2))_0^(c^2 // x) d x

int_a^b (c^4)/(2 x^2) d x = (- (c^2)/(2 x))_a^b = (- (c^2)/(2 b) + (c^2)/(2 a)) = (c^2 (b - a))/(2 a b)

Passo 3

Já a integral do denominador é exatamente a área da nossa seção. Portanto,

int_A^() d A = int_a^b int_0^(c^2 // x) d y d x

int_a^b (y)_0^(c^2 // x) d x

int_a^b (c^2)/(x) d x = c^2 (ln x)_a^b = c^2 (ln b - ln a) = c^2 ln ((b)/(a))

E por fim, o centroide será dado por:

overset(-)(y) = ((c^2 (b - a))/(2 a b))/(c^2 ln ((b)/(a)))

overset(-)(y) = ((b - a))/(2 a b ln ((b)/(a)))

E assim finalizamos a questão!

Resposta

overset(-)(y) = ((b - a))/(2 a b ln ((b)/(a)))

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centroide da área mostrada na figura por integração direta. (Cuidado: Observe cuidadosamente o sinal correto da raiz envolvida.)
Calcule a distância h - medida desde a base até o centroide do volume do cone circular truncado.
A figura representa uma peça plana de uma chapa metálica, simétrica em relação ao eixo A-A e que tem o contorno superior parabólico. Escolha as suas próprias coordenadas e calcule a distância h - a pa
Determine a coordenada y do centroide da área sombreada mostrada. (Observe os cuidados citados no Prob. 5/28).
Determine a coordenada x do centroide do segmento esférico sólido.