Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 27

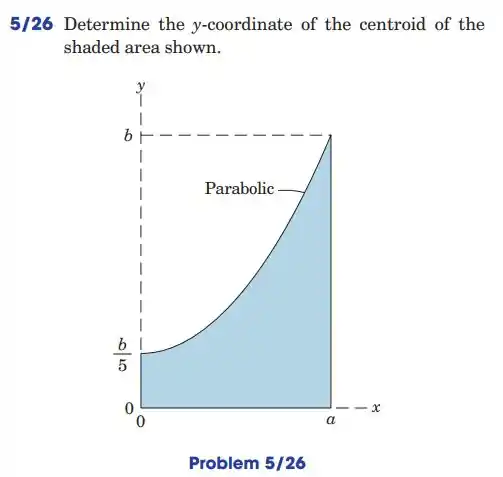
5.27. If the shaded area of Prob. 5/26 is rotated about the y-axis, determine the y-coordinate of the centroid of the resulting volume.

Passo 1

Vamos lá, temos um paraboloide e queremos descobrir o centro de massa no eixo y , e para isso vamos usar a equação

y - = ∫ y c d V V

Vamos usar volume aqui porque a parábola foi rotacionada, formando assim um objeto com 3 dimensões.

Primeiro vamos descobrir o elemento de área d V .

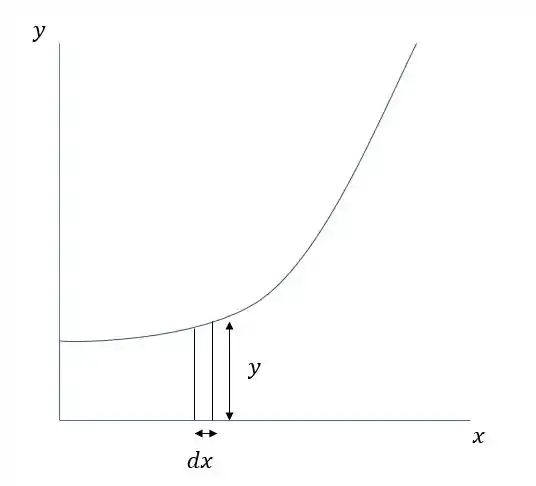
Então

d V = y   d A

Aqui d A não é a mesma que o problema anterior, é a área do círculo que vai se formar na base.

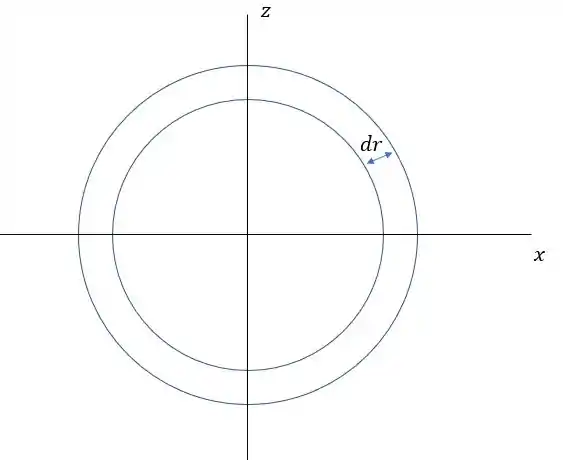
Esse elemento de área é

d A = 2 π r d r

Então

d V = y   2 π r   d r

E vamos resgatar a equação do problema anterior:

y = b 5 + 4 5 b a 2   x 2

Essa é a equação da parábola.

Então

d V = b 5 + 4 5 b a 2   x 2 2 π r d r  

Aqui podemos fazer a transformação

x = r

E ficamos com

d V = b 5 + 4 5 b a 2   r 2 2 π r d r  

d V = b 5 r + 4 5 b a 2   r 3 2 π   d r  

Passo 2

Agora vamos achar o volume dessa figura.

V = ∫ d V

Então

V = ∫ b 5 r + 4 5 b a 2   r 3 2 π   d r

V = 2 π ∫ b 5 r + 4 5 b a 2   r 3 d r

Os limites ficam os mesmos que seriam para x , mas agora para r

V = 2 π   ∫ 0 a b 5 r + 4 5 b a 2   r 3 d r

Então

V = 2 π b 10 r 2 + 4 20 b a 2 r 4 0 a  

V = 2 π b a 2 10 + 4 20 b a 2

Então o volume é:

V = 3 π a 2 b 5

Passo 3

O centroide da área é y C = y 2 , então nossa integral fica

y - = ∫ y c V d V

y - = ∫ 0 a y 2 3 π a 2 b 5 y   2 π r   d r

y - = 5 3 a 2 b ∫ 0 a y 2 r   d r

E finalmente temos

y - = 5 3 a 2 b ∫ 0 a b 5 + 4 5 b a 2   r 2 2 r   d r

Vamos desenvolver esse quadrado

y - = 5 3 a 2 b ∫ 0 a b 2 25 + 16 25 b 2 a 4 r 4 + 8 25 b 2 a 2 r 2   r   d r

y - = 5 3 a 2 b ∫ 0 a b 2 25 r + 16 25 b 2 a 4 r 5 + 8 25 b 2 a 2 r 3   d r

Resolvendo essa integral aqui

y - = 5 3 a 2 b b 2 50 r 2 + 16 150 b 2 a 4 r 6 + 8 100 b 2 a 2 r 4 0 a

Substituindo os valores

y - = 5 3 a 2 b b 2 a 2 50 + 16 150 b 2 a 2 + 8 100 b 2 a 2

Vamos colocar b 2 a 2 em evidencia

y - = 5 b 2 a 2 3 a 2 b 1 50 + 16 150 + 8 100

E finalmente temos

y - = 5 b 3 1 50 + 16 150 + 8 100 = 31 90 b

Resposta

y - = 31 90 b

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12- Determine as coordenadas x e y do centroide da área sombreada.
10- Determine a distância z - desde o vértice do cone circular até o centroide de seu volume.
11- Determine as coordenadas x e y do centroide da área trapezoidal.
15- A massa por unidade de comprimento da barra esbelta varia com a posição de acordo com ρ = ρ 1 - x 2 , onde x está em metros. Determine a localização do centro de massa da barra.
13- Localize o centroide da área sombreada