Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 29
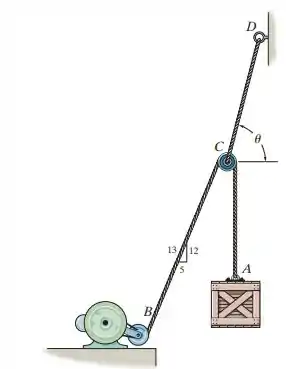
3.29. As cordas BCA e CD podem suportar, cada uma, uma carga máxima de . Determine o peso máximo da caixa que pode ser içada em velocidade constante e o ângulo θ para o equilíbrio. Despreze a dimensão da polia em C.
Passo 1
Falaaa! A gente quer achar a massa da caixa o ângulo para essa situação. A parada é começar fazendo o diagrama de corpo livre:
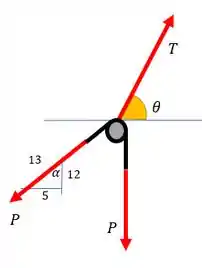
Vamos observar umas coisinhas.
Primeiro, como a caixa tem o peso , a corda que a puxa pela polia vai ter esse mesmo peso.
Outra coisa, se temos essas duas forças apontadas para baixo, com certeza precisa ser maior que elas, logo
Então é a força máxima que a gente tem na corda. Logo já podemos dizer de cara, que na situação limite (a que procuramos)
Repare que mesmo que a caixa esteja em movimento sua velocidade é constante, em outras palavras, não tem aceleração, então de acordo com a segunda lei de Newton, temos
A ideia é achar o que falta pelas equações de equilíbrio, já que as resultantes nos eixos zeram. Bora!
Passo 2
Beleza, vamos começar aplicando a condição de equilíbrio no eixo x
Mas pelo triângulo que nos é dado podemos determinar
Então
Passo 3
Agora para o eixo y
De novo vamos usar o triângulo
Então
Passo 4
Agora nós temos duas equações e duas incógnitas
Para encontrar P podemos sumir com elevando as equações ao quadrado e somando tudo
Passo 5
Agora que já determinamos o peso podemos usar qualquer uma das equações para achar θ