Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 7.Problemas - Ex. 49
Determine os diagramas de esforço cortante e de momento fletor para a viga com extremidade em balanço.
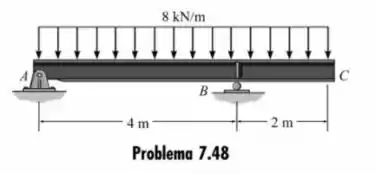
Passo 1
Salve salve galerinha, tudo beleza?
Vamos começar com o nosso D.C.L da viga
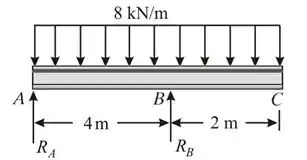
Esse problema aqui quer que encontremos o esforço cortante e o momento fletor.
Então observando rapidamente, podemos notar que o corpo encontra-se em equilíbrio, então a gente vai usar a equação de equilíbrio, pois a soma das forças e dos momentos são .
Mas vamos logo calcular as forças de reação em e .
Para isso, vamos considerar o eixo de rotação, assim:
Aplicando o equilíbrio de forças na direção y
Passo 2
Para AB:
Aplicaremos equilíbrio de forças na direção y:
Assim, encontramos que:
A força de cisalhamento um pouco antes de B
(Obs: estamos encontrando tudo que vem antes de B, logo após iremos encontrar tudo que vem depois de B).
Tomemos um momento sobre o ponto A
Tomemos um momento sobre o ponto B
Passo 3
Para
Iremos aplicar equilíbrio de forças na direção y
Força de cisalhamento logo, depois de B
Tomemos um momento sobre o ponto A
Passo 4
O momento fletor atinge o valor máximo com força cortante zero. Agora, partindo da função de cisalhamento na região AB, a força de cisalhamento zero está localizada em:
Logo, o valor do momento máximo é
Passo 5
Agora os diagramas de força cisalhante e momento fletor
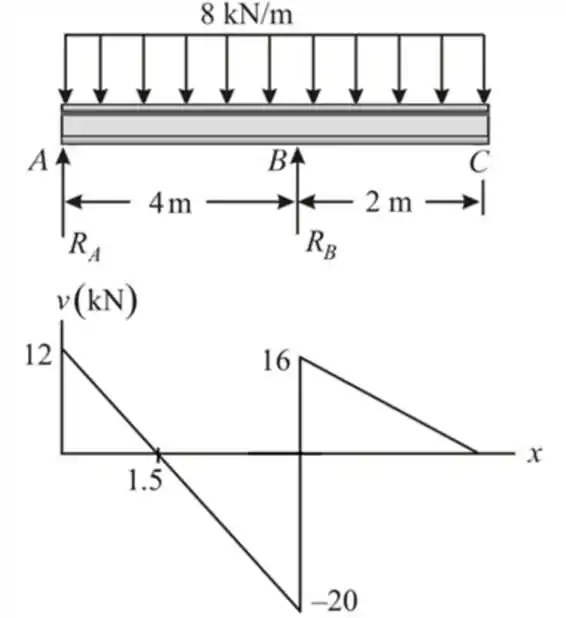
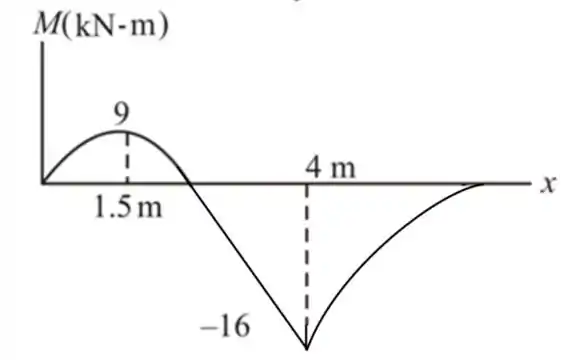
Resposta
Região :
Região :