Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 72
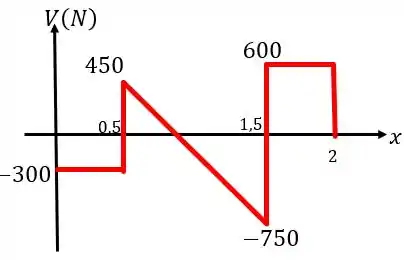
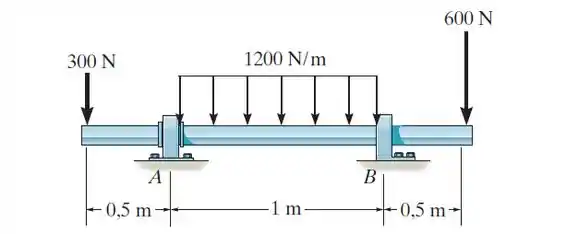
Determine os diagramas de força cortante e de momento fletor para a viga. Os apoios em e são um mancal axial e um mancal radial, respectivamente.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar os diagramas de força cortante e de momento fletor da viga. Para isto, vamos começar desenhando o diagrama de corpo livre da nossa viga. Esboçando-o, temos:
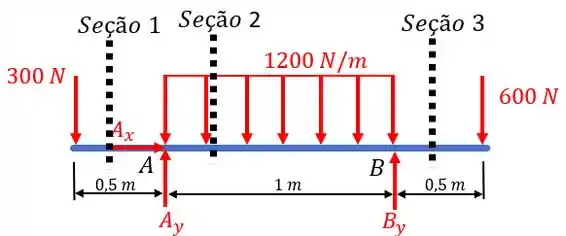
Como o mancal em é axial, ele tem reações em ambas as direções. Já o mancal radial em possui apenas uma direção normal na vertical.
Agora que obtemos o diagrama de corpo livre, precisamos analisar cada seção (indicada no nosso esboço pelas linhas tracejadas) e obter as equações para o esforço cortante e momento fletor.
Passo 2
Antes de calcularmos os esforços cortantes e momento fletor de cada seção, vamos determinar as reações , e dos mancais.
Para isto, basta aplicarmos as equações de equilíbrio. Logo,
Resolvendo o sistema acima temos , e
Passo 3
Vamos começar pela seção 1. Fazendo um corte nesta seção, teremos o seguinte diagrama:
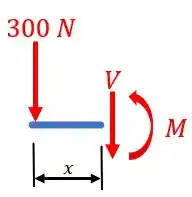
Sendo .
Agora, só precisamos aplicar as equações de equilíbrio. Portanto:
E chegamos a e .
Passo 4
Vamos agora para seção 2. Fazendo um corte nesta seção, teremos o seguinte diagrama:
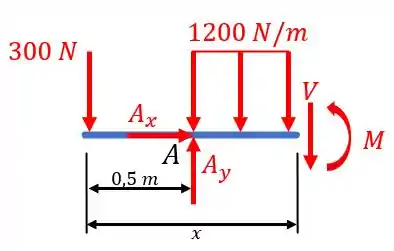
Sendo .
Agora, só precisamos aplicar as equações de equilíbrio. Portanto:
E assim chegamos as relações e .
Passo 5
Vamos agora para seção 3. Fazendo um corte nesta seção, teremos o seguinte diagrama:
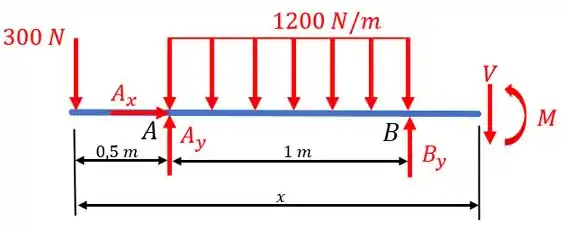
Sendo .
Agora, só precisamos aplicar as equações de equilíbrio. Portanto:
E assim obtivemos as últimas relações de momento fletor e esforço cortante.
Passo 6
Para finalizarmos a questão basta juntarmos todas as informações em um único gráfico. Começando pelo diagrama de esforço cortante, temos:
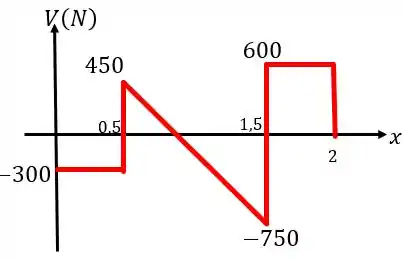
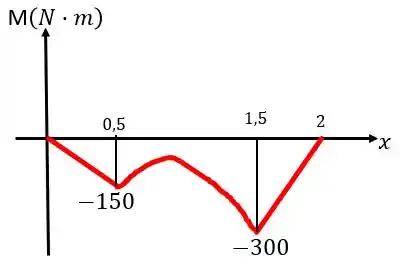
E o diagrama de momento fletor será:
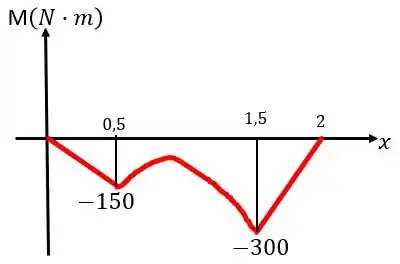
E assim finalizamos a questão!
Resposta
