Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 52
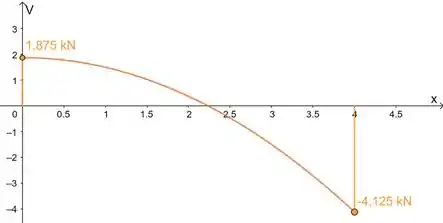
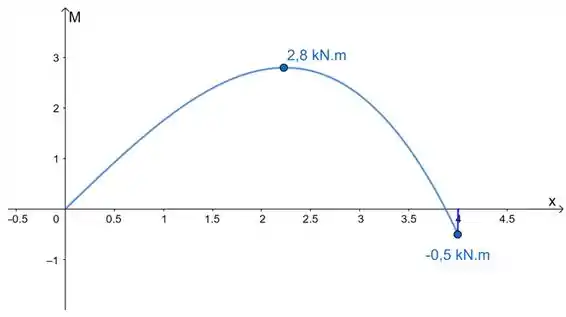
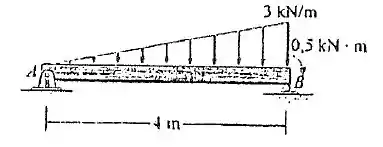
Determine os diagramas de esforço cortante e de momento fletor para a viga simplesmente apoiada.
Passo 1
Fala!
O problema quer que encontremos os diagramas do esforço cortante e do momento fletor. Vamos fazer isso achando as equações e .
A gente precisa começar achando as reações de apoio.
Então observando rapidamente, podemos notar que o corpo encontra-se em equilíbrio, então a gente vai usar a equação de equilíbrio, pois a soma das forças e dos momentos são . Vamos logo calcular as forças de reação em e .
Para isso, vamos considerar o eixo de rotação e o sentido anti-horário positivo, assim:
E a soma das forças:
Logo:
Prontinho! Agora a gente pode partir para achar e . Para isso, precisamos dividir nossa viga em intervalos. A divisão ocorre onde há mudanças no carregamento. Mas repara que sobre toda viga temos o mesmo carregamento linear, então só teremos um intervalo mesmo.
Vamos lá!
Passo 2
A ideia é cortar nosso intervalo em uma seção genérica distante de , e olhar para a esquerda. Aí a gente posiciona e nos sentidos positivos da conveção. E acha suas expressões pelas equações de equilíbrio. Nosso DCL:
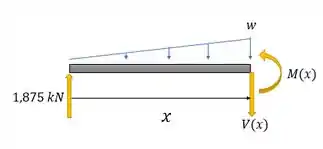
Antes de começar, a gente precisa descobrir aquele ali. Ele não é o do desenho do enunciado, porque a gente cortou nossa viga. Podemos acha-lo por semelhança de triângulos. Assim:
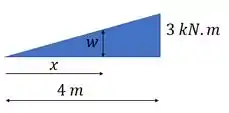
Passo 3
Agora sim! Bora montar nossas equações.
Para isso, vamos levar lembrar que a viga tá em equilíbrio assim:
Assim, encontramos que:
E se pegamos o somatório dos momentos, considerando o sentido anti-horário constante
Passo 4
Com esses dados e as equações, esboçamos os diagramas:
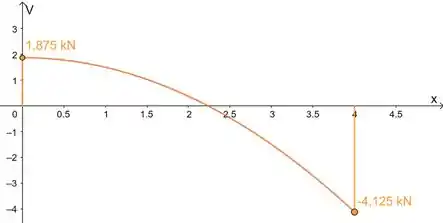
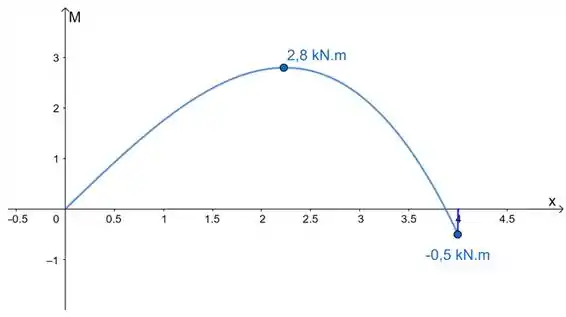
Resposta
