Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 38
A barra uniforme OA tem um peso de 100 N e quando ela está na posição vertical, a mola está livre. Determine a posição para o equilíbrio. Investigue a estabilidade na posição de equilíbrio.
Passo 1
Desenhando o diagrama do corpo livre:
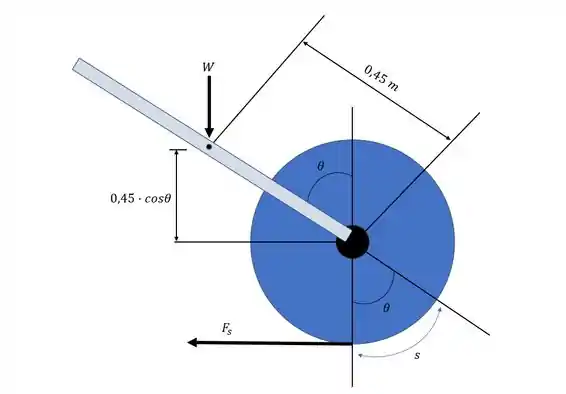
Passo 2
Começamos calculando a elongação da mola:
Passo 3
Calculamos a energia potencial elástica da mola (k=400 N/m do enunciado):
Passo 4
Calculando a energia potencial total do sistema temos:
Passo 5
Para encontrar a posição de equilíbrio, devemos encontrar a primeira derivada:
Passo 6
Para analisar a estabilidade, devemos calcular a expressão da segunda derivada:
Resposta
Exercícios de Livros Relacionados
39- A barra uniforme de massa m e comprimento l é articulada em relação a um eixo horizontal que pela sua extremidade O e está presa a uma mola de torção, que exerce um torque M = K θ sobre ela, onde
40- Determine, para um dado valor de θ , a força P necessária para manter o equilíbrio do mecanismo acionado por uma mola. A mola tem uma rigidez k e não está comprimida em θ = 0 . A massa dos element
43- Para o dispositivo mostrado, a mola não estaria esticada na posição θ = 0 . Especifique a rigidez k da mola que estabelecerá uma posição de equilíbrio θ no plano vertical. A massa das conexões é d
44- A mola de rigidez k não está comprimida quando u = 0 . A medida que u aumenta, a barra desliza dentro do anel articulado em A e comprime a mola situada entre o anel e a extremidade da barra. Deter
45- Um dos requisitos críticos no projeto de uma perna artificial é prevenir que a junta do joelho flambe sob carga quando a perna está esticada. Como uma primeira aproximação, simule a perna artifici