Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 61
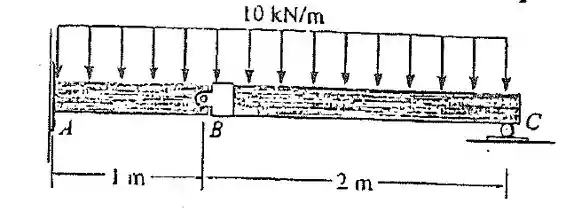
A viga composta tem apoio fixo , vinculação com pino em e é suportada por um rolete em . Determine os diagramas de esforço cortante e momento fletor para a viga.
Passo 1
Falaa! O problema quer que a gente encontre o diagrama de esforço cortante e o momento fletor. Mas repara que temos uma viga com engaste (reação vertical e de momento) numa extremidade e um apoio de primeiro gênero no outro (uma reação vertical).
Só que temos um pino em . Vamos começar encontrando as reações nos pinos e .
Como a viga é composta, a gente vai dividir em duas partes, e . A parte não fica em pé sozinha, então a gente vai começar por ela.
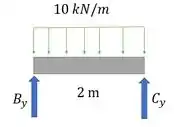
Pela simetria, vemos que . Aí:
Agora vamos para a parte :
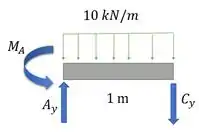
Calculando
Prontinho!
Passo 2
Aí agora a gente precisa achar as equações de e para cada parte dessa viga, e . Podemos olhar para cada uma separadamente.
Vamos começar por . Nossa seção vai estar a uma distância da extremidade . Vamos olhar para a parte esquerda da viga, colocar os esforços positivos nessa seção e descobrir o valor deles.
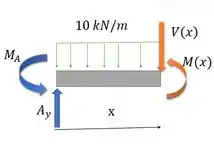
Vamos usar as equações do equilíbrio:
O momento na nossa seção:
Passo 3
Vamos olhar para . Essa é a viga com a seção em . Ela dista de .
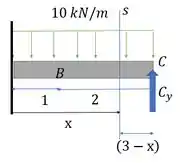
Para facilitar nossa vida a gente pode olhar a direita de :
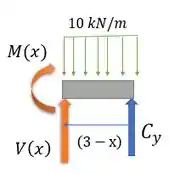
Usando as equações de equiíbrio
Passo 4
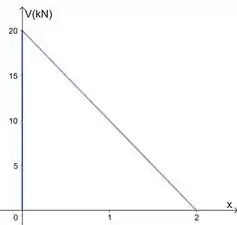
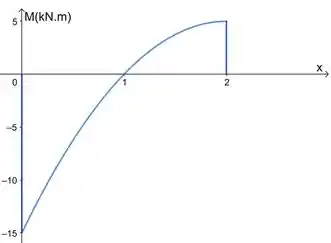
Agora a gente esboça essas funções respeitando os intervalos:
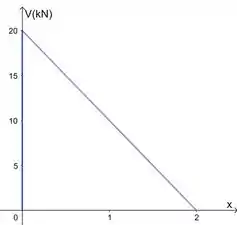
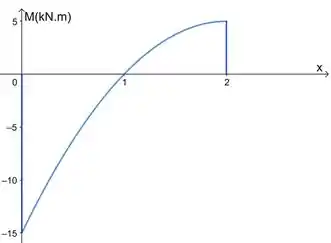
Repara que o momento no pino em é . Isso deve ocorrer mesmo.
Obs: os valores do gabarito são só para cê conferir se seu diagrama ficou certinho, tá? A resposta é esses gráficos que fizemos.
Resposta
