Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 104b
A barra AB consiste em duas porções, AC e CB, cada uma com 200 mm de comprimento e de área da seção transversal. A porção AC é feita de um aço doce com e , a porção CB, de um aço rápido com e Üma carga P é aplicada em C, como indicado. Pede-se:
(a) Assumindo que ambos os aços são elastoplásticos, desenhe o diagrama carga-de-flexão para o ponto C;
(b) Se P cresce gradualmente desde zero, determinar a máxima deflexão em C, a máxima tensão em cada porção da barra e a deflexão permanente do ponto C.
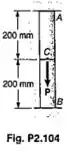
Passo 1
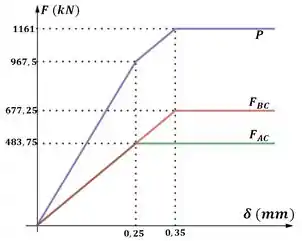
Com as informações dadas na questão, não é possível definir numericamente o valor da deformação máxima.
Então vamos expressar a deflexão máxima em termos das deformações de cada barra.
Passo 2
A máxima tensão possível é quando as barras atingem o regime plástico. Nesse ponto a tensão é sempre igual a tensão de escoamento:
Passo 3
A deflexão permanente é mais fácil de ser observada no gráfico.
Quando as forças forem aliviadas, a barra AC irá se recuperar de acordo com a linha verde pontilhada, e a barra irá se recuperar de acordo com a linha vermelha pontilhada.
Assim, somando as duas linhas pontilhadas encontramos a linha pontilhada roxa, que representa a forma como o ponto C irá se recuperar;
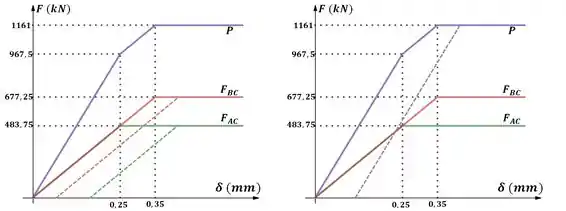
Essa linha pontilhada roxa é paralela a primeira região da curva roxa. Então, usando semelhança de triângulos podemos calcular a deformação recuperada do ponto C.
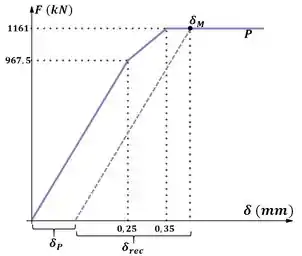
Assim, a deformação permanente será:
Passo 4
Resposta
Ei, a resposta está no passo a passo :)