Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 104a

A barra AB consiste em duas porções, AC e CB, cada uma com 200 mm de comprimento e 1935   m m 2 de área da seção transversal. A porção AC é feita de um aço doce com E = 200   G P a e σ 2 = 250   M P a , a porção CB, de um aço rápido com E = 200   G P a e σ e = 350   M P a . Üma carga P é aplicada em C, como indicado. Pede-se:

(a) Assumindo que ambos os aços são elastoplásticos, desenhe o diagrama carga-de-flexão para o ponto C;

(b) Se P cresce gradualmente desde zero, determinar a máxima deflexão em C, a máxima tensão em cada porção da barra e a deflexão permanente do ponto C.

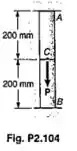
Passo 1

Se fizermos o diagrama de corpo livre das duas seções da barra veremos que um dos lados está sobre tração e o outro sobre compressão:

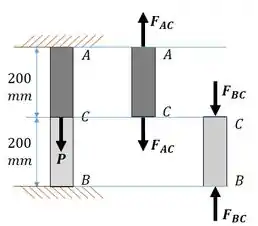
Note que esta é uma situação estaticamente indeterminada, então não podemos calcular as forças por enquanto.

Passo 2

Para gerar o gráfico Carga-Deformação, basta saber que o comportamento é crescente até o ponto de escoamento, e que depois disso a carga se mantém constante.

Primeiro vamos usar a lei de Hooke para determinar a deflexão no ponto de escoamento:

σ e A C = E ε e A C ⟹ ε e A C = σ e E = 250   M P a 200   G P a

ε e A C = 1,25 ⋅ 10 - 3

Logo:

δ e A C = ε e A C ⋅ L A C = 1,25 ⋅ 10 - 3 ⋅ 200 m m = 0,25   m m

E usamos a fórmula da tração para determinar a carga de escoamento:

σ e A C = F A C A ⟹ F A C = σ e A C ⋅ A = 250   M P a ⋅ 1935   m m 2

F A C = 483,75   k N

E geramos o gráfico:

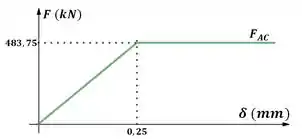
Passo 3

E vamos fazer o mesmo para a barra BC

Encontramos a deformação de escoamento:

ε e B C = σ e E = 350   M P a 200   G P a = 1,75 ⋅ 10 - 3

Logo:

δ e B C = ε e B C ⋅ L B C = 1,75 ⋅ 10 - 3 ⋅ 200 m m = 0,35   m m

E a carga de escoamento:

F e B C = σ e A = 350   M P a ⋅ 1935   m m 2 = 677,25   k N

Geramos o gráfico:

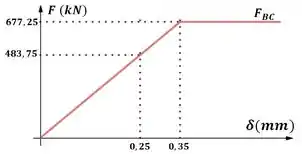
Passo 4

Agora que já temos os gráficos das duas seções:

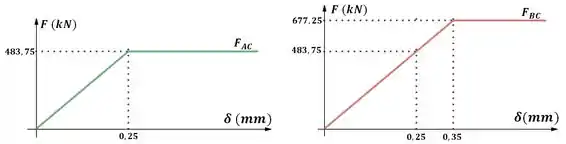
Vamos somar os pontos dos dois gráficos e obteremos o gráfico total do ponto C:

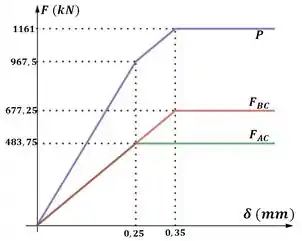
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na montagem mostrada, o membro B C é uma barra maciça de aço de 25,5m m de diâmetro e todos os outros membros são feitos de aço de 12,7m m . Usando-se E = 200G P a , determinar a deflexão do ponto D ,
Para a treliça e carregamento indicado no Prob. 10.27, determinar a deflexão vertical do ponto C .
Para a treliça e carregamento indicado no Prob. 10.29, determinar a deflexão vertical do ponto C .
O membro cilíndrico A B , vazado e de paredes finas, tem uma seção transversal não-circular e espessura não uniforme. Usando a expressão τ dada na Eq. (3.53), da Sec. 3.13, e a expressão para densidad
Cada membro da treliça mostrada é feito de aço e tem uma seção transversal de área igual a 3230m m 2 . Usando-se E = 200G P a , determinar a deflexão vertical do ponto B , provocada pela carga de 90k