Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 13
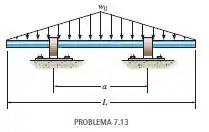
Determine a distância entre os mancais em termos do comprimento do eixo, de modo que o momento fletor no eixo simétrico seja zero no seu centro. A intensidade da carga distribuída no centro do eixo . Os suportes são mancais radiais.
Passo 1
Opaaa... beleza??
Antes de mais nada vamos já fazer o diagrama de corpo livre:
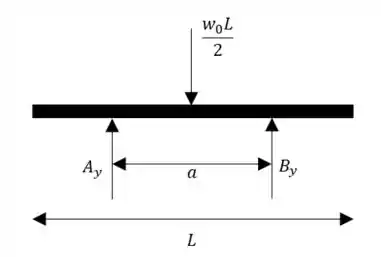
Lembrando que podemos substituir essa carga distribuída por uma carga pontual equivalente e que, como tem o formato de um triângulo, então fica:
Nessa questão vamos precisar dos conceitos de estática de que o somatório das forças em é igual a zero:
E o momento também é zero:
Passo 2
Para achar as reações de apoio fazemos o somatório das forças em
Pela simetria do problema:
Então:
Passo 3
Cortando beeem no meio, já que o momento fletor no eixo seja zero no seu centro:
Se liga só que agora precisamos mudar o ponto da carga pontual equivalente (como a carga distribuída bem o formato de um triângulo, então ela fica a e não na metade).
Para não precisar calcular a força cortante , vamos fazer o balanço de momento nesse ponto mesmo:
Como :
Opaaa... e acabamos mais uma. Desanima não. Toma uma água e bora pra próxima... =)