Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 18
Determine as forças normal e cortante e o momento fletor ponto .
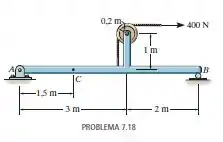
Passo 1
Opaaa... belezinha?
Nessa questão vamos precisar dos conceitos de estática onde:
- o somatório das forças em é igual a zero:
- em
- e o momento também:
Vamos já lançar esse diagrama de corpo livre brabo:
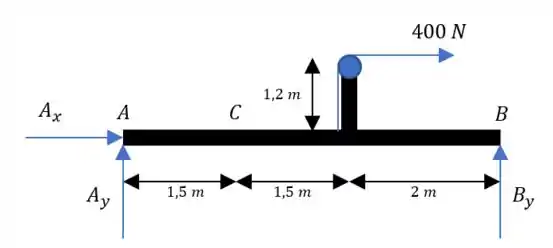
Passo 2
Fazendo o somatório das forças em :
O somatório das forças em :
E do momento:
Passo 3
Fazendo o corte em :
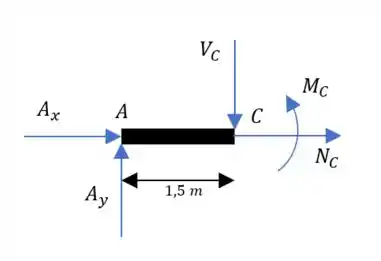
Para o somatório das forças em :
Em
E, finalmente, o momento:
Essa foi, né? Então vamos pra mais uminha...
Resposta
Exercícios de Livros Relacionados
A lança do guindaste suporta uma carga de 3,75k N através do carrinho que desliza por cima da lança. Determine a força normal interna, o esforço cortante e o momento no ponto D da lança quando o carri
O macaco A B é usado para acertar a viga fletida D E usando a montagem mostrada. Se a força compressiva axial no macaco é de 25k N , determine o momento interno desenvolvido no ponto C da viga superio
Determine as componentes x , y e z da carga interna em uma seção passando pelo ponto C na tubulação. Despreze o peso da tubulação. Faça F 1 = 350 j - 40 0 kk N e F 2 = 15 0 i - 300 kk N .
Determine a força normal interna, o esforço cortante e o momento nos pontos F e G da viga composta. O ponto F está localizado à direita da força 2,5k N , enquanto o ponto G está localizado à direita d
A lança do guindaste suporta uma carga de 3,75k N através do carrinho que desliza por cima da lança. Determine a força normal interna, o esforço cortante e o momento no ponto C da lança quando o carri