Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 7.Problemas - Ex. 41
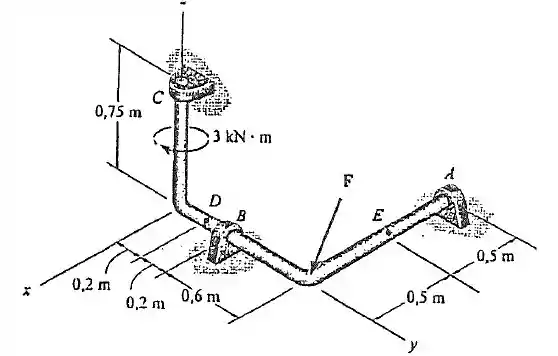
38. Determine as componentes e da carga interna no ponto da barra. Existem mancais radias em e . Considere .
Passo 1
Fala meu querido, a gente quer os esforços internos em . Tá aqui o passo a passo que vamos usar resumido para ti:
Para resolver esse problema primeiro temos que determinar as forças que atuam em e referentes ao mancal, em teremos e , em teremos e , em teremos e .
Para completar a análise do problema vamos cortar nossa estrutura em , e olhar só para a parte a esquerda desse ponto. Aí nós vamos posicionar as componentes dos esforços internos nessa seção.
Tendo isso, vamos usar as equações de equilibro para seção mencionada anteriormente, e vamos achar os valores de e que serão forças cortantes, que será nossa força normal, nosso momento torsor e e nossos momentos fletor.
Vamos adotar o sentido anti-horário como o positivo quando formos calcular momentos nesse rolê aí, tá? Bora lá começar!
Passo 2
Vamos aplicar as equações de equilíbrio do momento e da força, no esquema completo da figura, sem ela estar cortada, para achar as reações.
Começando pelos momentos:
Calculando o somatório de forças nos eixos:
Com essas equações temos o seguinte sistema:
Resolvendo esse sistema, temos:
Passo 3
Agora vamos aplicar as equações de equilíbrio referentes a força para parte seccionada à esquerda de . Por que à esquerda? Porque essa parte tem menos carregamentos, aí é mais simples.
Vamos posicionar nossos esforços internos na seção e calcular seus valores:
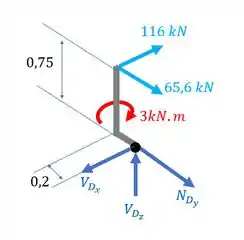
Agora para o eixo :
E agora o eixo :
Passo 4
Agora vamos aplicar as equações de equilíbrio referentes ao momento para parte seccionada à esquerda de .
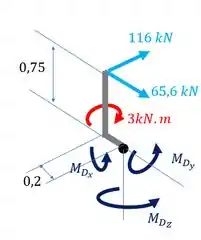
Para o eixo :
E para o eixo