Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 100
Determine a distância para que a parte do cabo seja horizontal, os componentes correspondentes da reação em .
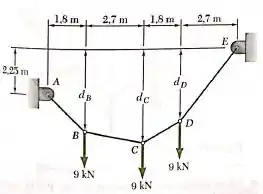
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Analisando a parte , temos que:
Calculando o momento no ponto , temos:
Passo 2
Agora, vamos analisar o cabo inteiro fazendo o momento em .
Logo:
Resposta
Exercícios de Livros Relacionados
A viga A B , que está sujeita ao carregamento uniformemente distribuído mostrado na figura e a duas forças desconhecidas P e Q . Sabendo que foi experimentalmente determinado que o momento fletor é +
A viga A B , está sujeita ao carregamento uniformemente distribuído mostrado na figura e a duas forças desconhecidas P e Q . Sabendo que foi experimentalmente determinado que o momento fletor é + 8 ,
Resolva o Problema 7.91 , considerando que o momento fletor que foi encontrado era + 8k N ⋅ m em D e + 9,2k N ⋅ m em E .
Resolva o Problema 7.89 , considerando que o momento fletor que foi encontrado era + 650N ⋅ m em D e + 1450N ⋅ m em E .
Sabendo que P = Q = 675N , determine a a distância a para a qual o valor absoluto máximo do momento fletor na viga A B é o menor possível, b o valor correspondenete de M m á x á . (Ver dica do Problem