Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 60

Sabendo que P = Q = 675   N , determine a a distância a para a qual o valor absoluto máximo do momento fletor na viga A B é o menor possível, b o valor correspondenete de M m á x . (Ver dica do Problema 7.55 .

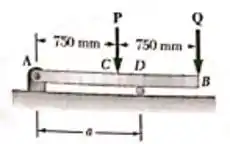
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Observe o diagrama:

Vamos fazer o somatório de momento em A para encontrar a reação R D .

∑ M A = 0

R D a - P 0,75 - Q 1,5 = 0

R D = 1518,75 a

Aplicando o somatório de forças em y , temos:

∑ F y = 0

R A y - 675 - 675 + 1518,75 a = 0

R A y = 1350 - 1518,75 a

Passo 2

Agora vamos analisar o momento em C .

∑ M C = 0

- 1350 - 1518,75 a 0,75 + M = 0

M = 1012,5 - 1139,0625 a

Agora em D , temos:

∑ M D = 0

- 675 1,5 - a - M = 0

M = 675 a - 1012,5

Passo 3

Equacionando, temos:

2025 - 1139,0625 a = 675 a - 1012,5

a = 1 , 3   m

Passo 4

Portanto o momento absoluto máximo é:

M m á x = - M D = - 675 1,5 - a

M m á x = - 675 1,5 - 1 , 3

M m á x = 135   k N ⋅ m

Resposta

a )   a = 1 , 3   m

b ) M m á x = 135   k N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cabo de comprimento L + Δ é suspenso entre dois pontos que estão na mesma elevação e que tem distância L entre si. (a) Considerando que Δ é curto comparado com L e que o cabo é parabólico, determin
Se a = 4m , determine as intensidades de P e Q necessárias para manter o cabo na forma mostrada na figura.
Cada cabo da ponte Golden Gate sustenta uma carga de w = 166,5k N / m ao longo da horizontal. Sabendo que o vão L é 1245m e que a flecha h é 139,2m , determine (a) a tração máxima em cada cabo (b) o c
O cabo A B sustenta uma carga uniformemente distribuida ao longo da horizontal, como mostra a figura. Sabendo que em B o cabo forma um ângulo θ B = 35 ° com a horizontal, determine (a) a máxima tensão
A massa total do cabo A C é 25k g . Considerando que a massa do cabo distribuída uniformente ao longo da horizontal. Determine a flecha h e a inclinação do cabo entre A e C .