Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 98
Determine a distância para que a parte do cabo seja horizontal, as correspondentes reações em e .
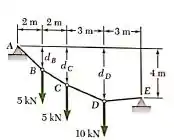
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Temos o seguir o diagrama de corpo livre da seção :
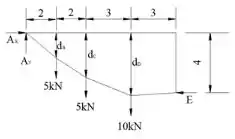
Calculando o momento no ponto , temos:
A reação no apoio pode ser determinada pelas equações de equilíbrio de força:
Passo 2
A dimensão é determinada usando o diagrama de corpo livre da seção :
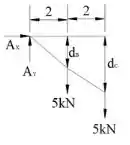
Fazendo o somatório de momentos no ponto , podemos determinar :
Passo 3
Agora que temos as componentes é só aplicar Pitágoras para descobrir o valor da reação.
Resposta
Exercícios de Livros Relacionados
Sabendo que d C = 3m , determine a as distâncias d B e d D , b a reação em E .
Determine a a distância d C para que a parte B C do cabo seja horizontal, b os componentes correspondentes da reação em E .
O cabo A B C sustenta duas cargas tal como mostra a figura. Sabendo que b = 1,2m , determine a a intensidade necessária da força horizontal P , b a distância correspondente a .
Sabendo que m B = 18k g e m C = 10k g , determine a intensidade da força P necessária para se manter o equilíbrio.