Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 101
O cabo sustenta duas cargas tal como mostra a figura. Sabendo que , determine a intensidade necessária da força horizontal , a distância correspondente .
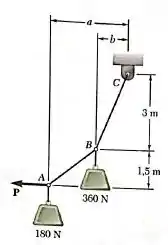
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Com o somatório das forças em , temos que:
Como o somatório dos momentos em , analisando o cabo , temos:
Passo 2
Agora, analisando somente a parte , horizontalmente, temos:
Ao calcular a distância correspondente , temos:
Resposta
Exercícios de Livros Relacionados
Para a viga do Problema 7.47, determine (a) a razão k = P / w a para a qual o valor absoluto máximo do momento fletor na viga é o menor possível, (b) o valor corresponde |M|max. (Ver dica do Problema
Para o elemento estrutural do Problema 7.50 determine a o ângulo θ para o qual o valor absoluto máximo do momento fletor na viga A B é o menor possível, b o valor correspondente de M m á x á . (Dica:
Para a viga mostrada na figura, determine (a) a intensidade P das duas forças direcionadas para cima para que o valor absoluto máximo do momento fletor na viga é o menor possível, (b) o valor correspo
A viga uniforme é levada por cabos de guindaste ligados em A e B. Determine a distância a das extremidades da viga ate os pontos onde os cabos devem ser ligados se o máximo valor absoluto do momento f
Duas cargas estão suspensas no cabo A B C D tal como mostra a figura. Sabendo que h B = 1,8m , determine a a distância h C , b os componentes da reação em D , c a tração máxima do cabo.