Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 31
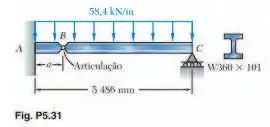
Determine (a) a distância para a qual o valor absoluto do momento fletor na viga é o menor possível e (b) a tensão normal máxima correspondente provocada pelo momento fletor. (ver sugestão do problema 5.27).
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Partiu outra questão.
Primeiramente, vamos pegar a parte Sabemos que, por simetria:
Aplicando aa equações de equilíbrio:
Agora, vamos encontrar a equação do momento no segmento estudado. Percorrendo o segmento e somando-se as parcelas do momento:
Para acharmos o mínimo da função, devemos derivá-la e igualá-la a 0. Fazendo isso:
Logo, o momento máximo será:
Passo 2
O próximo passo é calcular a equação do momento para o segmento Sabemos que:
Como é um engaste, o momento máximo ocorrerá em logo:
Passo 3
Usando a dica dada, vamos igualar os dois momentos. Teremos:
Resolvendo a equação:
Passo 4
Agora, devemos determinar a maior tensão normal na estrutura. Sabemos que a tensão normal é dada por:
O valor de é a distância da linha neutra e é o momento de inércia. Esses valores são tabelados para o perfil dado. Usando a tabela: