Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 82a

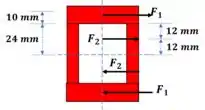
Resolver o Prob 4.80, considerando a viga do Prob 4.78

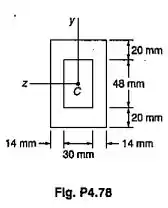
Passo 1

Para determinar o momento plástico, nós temos que considerar a situação em que toda a viga está sofrendo deformação plástica.

Vamos fazer um desenho, neste desenho as regiões plásticas estão em vermelho:

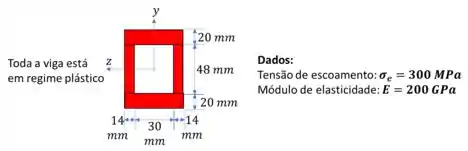
Ou seja, todas as regiões da viga estão sofrendo a tensão de escoamento!

Então, vamos usar o método do exercício 4.78b para determinar a tensão que atua na viga.

Passo 2

Para calcular o momento aplicado vamos voltar pra teoria das tensões. Observe a figura abaixo, na região plástica a tensão é constantemente igual a tensão de escoamento!

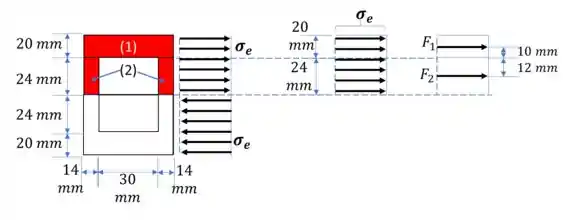
Vamos lembrar que a tensão é dada por σ = F A , e que a distribuição de tensão tem formato retangular! Com isso em mente, podemos calcular duas forças equivalentes às tensões.

F 1 = σ e A 1 = 300   M P a ⋅ 58   m m ⋅ 20   m m = 348   k N

F 2 = σ e A 2 = 300   M P a ⋅ 2 ⋅ 14   m m ⋅ 24   m m =   201,6   k N

Passo 3

Como a viga é simétrica, as regiões superior e inferior sofrem os mesmos esforços, porém, em tração ou compressão!

Essas forças formam binários, e a resultante destes binários é o momento sobre a viga.

M p = 2 ⋅ F 1 ⋅ 34   m m + 2 ⋅ F 2 ⋅ 12   m m

M p = 2 ⋅ 348   k N ⋅ 34   m m + 2 ⋅ 201,6   k N ⋅ 12   m m

M p = 28,5   k N m

Resposta

M p = 28,5   k N m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga em balanço AB consistindo em uma placa de altura constante h e largura b variável suporta a carga concentrada P no ponto A. (a) sabendo que a viga é de resistência constante, expresse b em te
Três placas de aço são soldadas juntas para formar a viga mostrada. Sabendo que a tensão normal admissível para o aço utilizado é de 22 ksi, determine a largura mínima b do flange que poderá ser usada
(a) Usando funções de singularidade, escreva as equações para a força cortante e o momento fletor para a viga ABC sob o carregamento mostrado. (b) Use a equação obtida para M para determinar o momento
(a) Usando funções de singularidade, escreva as equações para a força cortante e o momento fletor para a viga ABC sob o carregamento mostrado. (b) Use a equação obtida para M para determinar o momento
(a) Usando funções de singularidade, escreva as equações para a força cortante e o momento fletor para a viga e o carregamento mostrados. (b) Determine o valor máximo do momento fletor na viga.