Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 33
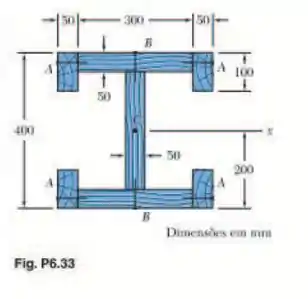
A viga mostrada na figura foi feita pregando-se várias tábuas e está sujeita a uma força cortante de 8 kN. Sabendo que os pregos estão espaçados longitudinalmente a cada 60 mm em A e a cada 25 mm em B, determine a tensão de cisalhamento nos pregos (a) em A e (b) em B. (Dado: = 1,504 x .)
Passo 1
Antes de começar esse exercício, é importante dizer que o que o enunciado está pedindo na verdade é a força de cisalhamento sobre os pregos, e não a tensão.
Beleza! Para encontrar a força de cisalhamento nos pregos em A e B, vamos utilizar a equação que fornece justamente esse valor, dada por:
Em que q é o fluxo de cisalhamento e s é o espaçamento entre os pregos, que foi dado no enunciado. Nós sabemos também que o fluxo de cisalhamento é dado por:
Em que V é a força cortante que foi dada no enunciado, Q é o momento de área e I é o momento de inércia da seção, que também foi dado no enunciado. Sendo assim, o que precisamos encontrar é o momento de área da seção com junta em A e da seção com junta em B
Passo 2
Tá legal! Vamos começar a letra (a) destacando a área onde temos a junta em A, da seguinte forma:
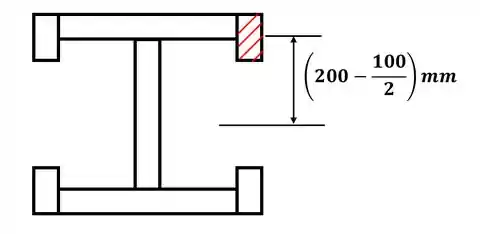
Note que já destacamos a distância entre o centroide da seção em análise e o centroide da seção transversal como um todo, pois vamos precisar dessa distância para calcular o momento de área da seção, que é dado por:
Então, para a área A, teremos:
Com esse valor podemos calcular o fluxo de cisalhamento na junta em A, dado por:
Substituindo os valores conhecidos, teremos:
E, com isso, conseguimos encontrar a força de cisalhamento nos pregos da junta A através de:
Substituindo os valores conhecidos, teremos:
Beleza! A letra (a) fechou!
Passo 3
Agora para a letra (b), vamos repetir os cálculos do passo 2, só que com a seguinte área de interesse:
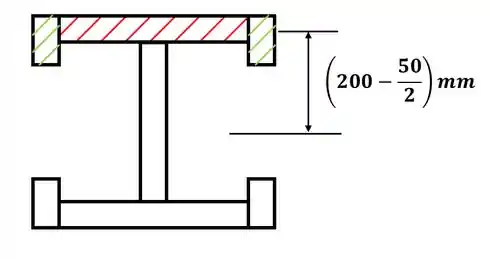
Note que já destacamos a distância entre o centroide da seção “b” (hachurada em vermelho) e o centroide da seção transversal como um todo, pois vamos precisar dessa distância para calcular o momento de área da seção, que é dado por:
Nesse caso, temos que considerar toda a porção superior da viga, que seriam as duas áreas “A” menores e a área “b” horizontal hachurada em vermelho. Então, para a área B, teremos:
Com esse valor podemos calcular o fluxo de cisalhamento na junta em B, dado por:
Substituindo os valores conhecidos, teremos:
E, com isso, conseguimos encontrar a força de cisalhamento nos pregos da junta B através de:
Substituindo os valores conhecidos, teremos:
Prooonto! Mais um exercício finalizado!