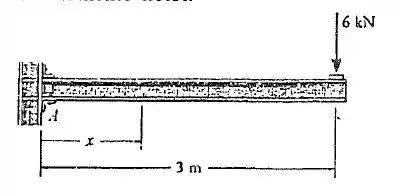
7. Determine o esforço cortante e o momento fletor como uma função de , e depois construa os diagramas de esforço cortante e de momento fletor.
Passo 1
Cara, o enunciado quer que a gente ache os diagramas de momento fletor e de cortante nessa viga.
Percebe que se a gente cortar essa viga no meio e olhar para a direita, todas as forças e carregamentos são conhecidos?
Cara, isso é um bizu que te dou: quando a viga só tem carregamentos nas extremidades, e você já conhece o valor deles em uma das extremidades, para achar as equações dos esforços, você não vai precisar achar as reações de apoio, ok?
E como a gente vai fazer?
Cara, a gente vai cortar nossa viga em uma seção distante de , e olhar só para a direita, onde conhecemos todos os carregamentos, assim:
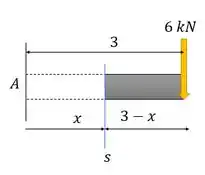
E aí determinamos e em . Bora lá!
Passo 2
Vamos posicionar as componentes de e na nossa seção, seguindo a orientação positiva convencionada. E aí a gente acha a expressão desses carinhas pelas equações de equilíbrio.
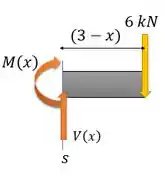
Então:
Calculando o somatório do momento na nossa seção , considerando o sentido horário positivo
Passo 3
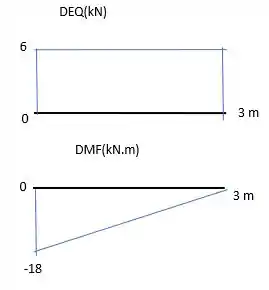
Agora vamos construir os diagramas de esforço cortante e momento fletor, para fazer isso, basta esboçar um gráfico da função que encontramos para cada um deles.
Abaixo encontrasse os gráficos.
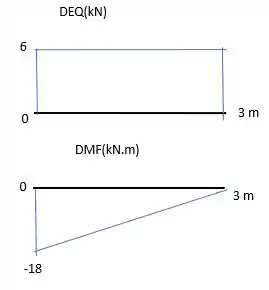
Resposta