Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 8.Problemas - Ex. 2

8.4. Se o coeficiente de atrito estático em A é μ s = 0,4 e o colar em B é liso, de modo que só exerce uma força horizontal sobre o cano, determine a distância mínima x de modo que a cantoneira possa suportar o cilindro de qualquer massa sem deslizar. Despreze a massa da cantoneira.

Passo 1

Vamos começar desenhando os diagramas de corpo livre.

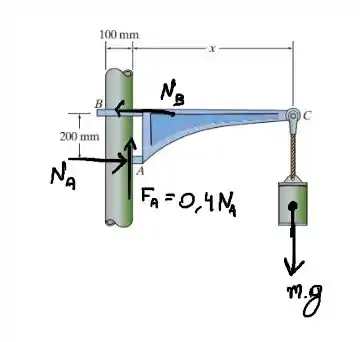
Passo 2

Agora vamos usar as equações de equilíbrio, para o primeiro caso temos

F R y = 0

F R y = 0,4 ⋅ N A - m ⋅ g = 0

Então

N A = 2,5 ⋅ m ⋅ g

Passo 3

Agora vamos usar a equação do momento no ponto B

M B = 0

M B = 2,5 ⋅ m ⋅ g ⋅ 0,2 + 0,4 ⋅ 2,5 ⋅ m ⋅ g ⋅ 0,1 - m ⋅ g ⋅ x + 0,1 = 0

Isolando x

m ⋅ g ⋅ x = 2,5 ⋅ m ⋅ g ⋅ 0,2 + 0,4 ⋅ 2,5 ⋅ m ⋅ g ⋅ 0,1 - m ⋅ g ⋅ 0,1

Perceba que o termo m ⋅ g pode ser cortado

x = 2,5 ⋅ 0,2 + 0,4 ⋅ 2,5 ⋅ 0,1 - 0,1 = 0,5   m

Repare que independe da massa do cilindro.

Resposta

x = 0,5   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco C tem uma massa de 50k g e está confinado entre duas paredes por roletes lisos. Se o bloco se apoia no topo do carretel de 40k g , determine a força P mínima do cabo necessária para mover o ca
A empilhadeira de 3M g tem centro de massa em G . Determine o maior número de caixas que podem ser empurrados pela empilhadeira se cada caixa tem uma massa de 500 k g . O coeficiente de atrito estátic
O utilitário com tração nas quatro rodas de 3M g tem centro de massa em G . Determine a massa máxima da tora que pode ser rebocada pelo automóvel. O coeficiente de atrito estático entre a tora e o sol
O bloco C tem uma massa de 50k g e está confinado entre duas paredes por roletes lisos. Se o bloco se apoia no topo do carretel de 40k g , determine os coeficientes de atrito estático exigidos em A e
Se o coeficiente de atrito estático nos pontos de contato A e B for μ s = 0,3 , determine a força máxima P que pode ser aplicada sem fazer com que o carretel de 100 k g se mova.