Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 10
Para o arco do Problema , determine a intensidade e a localização da foça axial máxima, do esforço cortante máximo do momento fletor máximo.
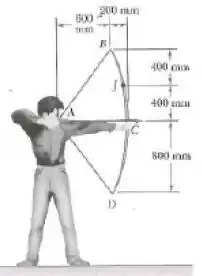
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Vamos calcular a reação no cabo do arco:
Em seguida, analisaremos as foças internas ao ponto :
A cortante será:
E:
Passo 2
Considerando o arco como uma parábola, temos que a equação da paránola é dada por:
Precisaremos então, de dois pontos para encontrar a equação:
O ângulo da força é dado por:
Passo 3
Vamos agora, calcular a força máxima. Para a equação da força, podemos considerar as parcelas normal e tangencial da força :
O maior valor para é quando , que ocorre no ponto :
A cortante máxima é dada por:
O maior valor de é quando há a maior concentração de forças agindo tangencialmente ao arco. Perceba que os cabos estão tracionando de forma tangencial nas pontas e . Portanto, aquela condição é a que apresenta maior concentração de forças cisalhantes.
Nesse ponto, a tensão cisalhante é igual à tração do cabo:
Sabemos também que o momento é máximo em , onde , logo: