Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 58
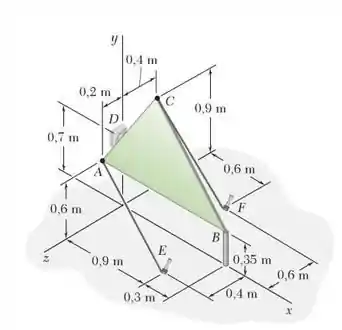
57. A placa triangular é sustentada por juntas rotuladas em e e mantida na posição mostrada pelos cabos e . Se a força exercida pelo cabo em é , determine o momento dessa força em relação a linha que une os pontos e .
Passo 1
Bom! Antes de mais nada, vamos definir a expressão de momento em relação a como sendo:
A primeira coisa é definir cada termo no seu quadrado. Olha só!!! Esse é definido a partir da seguinte relação:
Em seguida, vamos determinar a distância em termos dos vetores unitários e . Para fazer isso, basta observar a figura do enunciado. Veremos que o ponto está nas coordenadas em metros e o ponto, encontra-se nas coordenadas . Com isso, para achar basta fazer a diferença entre as coordenadas de e as coordenadas de :
E o valor de é dado por:
Logo, já podemos obter :
Depois continuemos à caça. O próximo passo é achar o vetor posição , que é dado pelo vetor :
Passo 2
Achada o nosso vetor e o valor de , falta apenas a força. Por isso vamos olhar a figura novamente; afinal vamos ter que tratar de decompor a força de tensão presente no cabo :
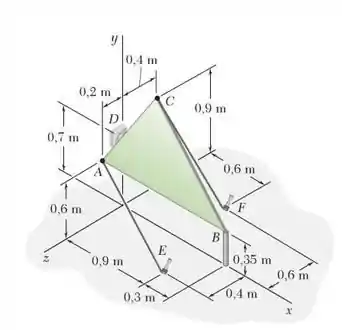
Para fazer isso, determinemos a distância em termos dos vetores unitários e . Vemos que o ponto está nas coordenadas em metros e o ponto, encontra-se nas coordenadas . Com isso, para achar , basta fazer a diferença entre as coordenadas de e as coordenadas de:
E precisamos também do valor de , em módulo, né?
Desse jeito, a nossa tração vai ser dada por:
Passo 3
Por fim, apliquemos a definição de momento:
Onde temos que:
Vamos então, fazer o produto vetorial usando o determinante matricial:
Esse é o nosso momento resultante!!