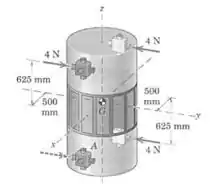
A nave espacial do Prob. está repetida aqui. A ideia é ligar quatro retrofoguetes de , como mostrado, para girar a nave em torno de seu eixo , mas o retrofoguete em falha. Determine o sistema força-binário equivalente em devido aos três retrofoguetes remanescentes.

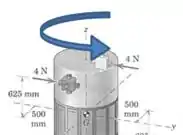
Agora queremos calcular o momento gerado por elas em relação ao ponto .

As forças vão favorecer a rotação em duas direções diferentes. Na primeira delas, que é em torno do eixo , todas as forças estão “colaborando, então podemos somar as três:

E é a distância perpendicular entre cada ponto de ação de força e o ponto .

Na segunda dessas direções, que é torno do eixo , temos duas forças “cooperando” no sentido horário (sinal negativo), e uma “atrapalhando” no sentido anti-horário (sinal positivo):

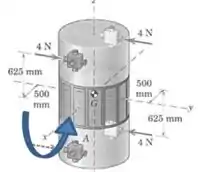
(O sentido da seta azul é só ilustrativo). Então essa componente do momento é:

E agora já podemos calcular o momento total: