Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 4
Determine a força em cada elemento da treliça carregada.
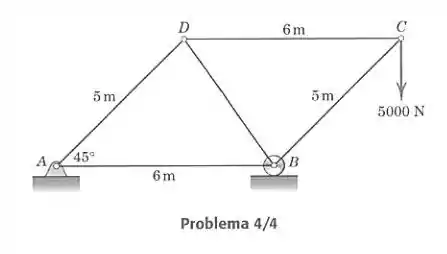
Passo 1
Fala galera boa, tudo bem com vocês? Calcular treliça tem que ficar no sangue, bora fazer mais esse pra melhorar essa habilidade?
O objetivo aqui é determinar a força normal, barra por barra. Se liga que o exercício não nos dá a distância do rolete em B até a força em C, nesse caso não é bom começar fazendo somatório de momento fletor.
Mas e agora, como eu começo? Bom a gente tem que procurar um nó que tenha uma incógnita a menos, traduzindo pra nossa língua um nó onde a gente consiga igualar o peso ou uma reação a alguma componente e o nó C é perfeito pra isso, veja:
Nó C:
A força em é de compressão, como mostra a figura.
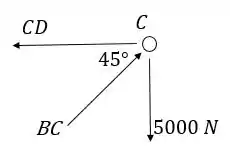
Fazendo o somatório das forças em y, encontramos FBC.
Fazendo o somatório das forças em x a gente tira FCD:
Passo 2
Nós, nós e mais nós, parece até que a gente tá amarrando alguma coisa né! A gente pode ir agora pro nó D, mas tem uma parada, precisamos saber de que ângulo vem as forças:
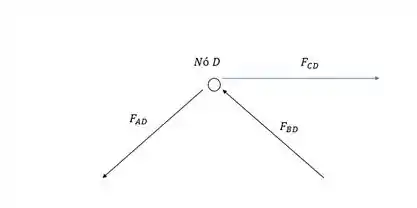
Bom, é de boa o ângulo da força FAD, tá ali na treliça como 45 graus, mas e FBD? Vamos precisar calcular o tamanho da barra BD e então calculamos o ângulo.
Usando a lei dos cossenos a gente encontra BD:
Substituindo:
Resolvendo, temos:
E com a lei dos senos a gente encontra o ângulo que vem a força BD:
Rearrumando:
Passo 3
Ufa, agora a gente pode enfim calcular as forças no nó D. Voltando para ele temos:
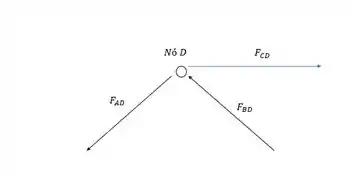
Com FCD= 5000N.
E fazendo o somatório das forças em y:
E em x:
Aqui tem um SUPER BIZU, não precisamos resolver esse sistema substituindo pois como o ângulo da força FAD, é 45 graus, basta subtrairmos a equação 1 da equação 2.
O primeiro termo vai á zero então e ficamos só com:
Voltando para a equação 1, a gente encontra FAD:
Passo 4
Chegando enfim ao nó A, a gente pode calcular a força na barra AB, mas antes é bom lembrar que nós não temos reação horizontal no pino A, se fizermos o somatório das forças em x na treliça veremos que:
Enfim, o nó A:
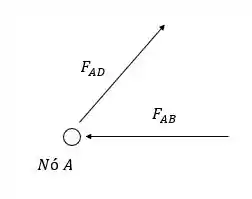
Fazendo o somatório das forças em x: