Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 11

Determine a força em cada membro da treliça e diga se os membros estão sob tração ou compressão. Faça e .

Passo 1

Falaa!

O problema que que a gente encontre a força de cada membro mostrando se ele está sendo tracionada ou comprimida. Nesse caso, vamos analisar junta por junta (Método dos nós).

É bom começar por nós onde a geometria já entrega o valor das forças. Repara.

Vamos começar pelo DCL do nó B:

Percebe que essas barras são perpendiculares, do somatório de forças nesses dois eixos perpendiculares já desenhados por elas, temos que

Fofo né, já achamos que uma força é zero. Isso aconteceu porque temos uma barra perpendicular a outras duas, sem nenhuma força externa aplicada.

Passo 2

Uma observação antes de ir para as outras, é que a gente vai achar o cosseno e seno referente as orientações das barras pela geometria das figuras, olhando triângulos visíveis na nossa estrutura, bele? Assim oh:

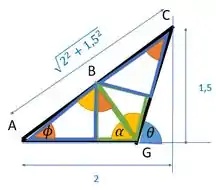
Daí a gente tira:

Como e formam :

E para a gente pode observar:

Pela simetria, acontece o mesmo do lado esquerdo da treliça.

Vamos seguir!

Passo 3

Então, vamos para as forças da junta , porque tem apenas duas forças desconhecidas e possui uma que sabemos ser . Sabendo que o somatório das forças no eixo e somatório das forças do eixo é , pois a estrutura encontra-se em equilíbrio.

No eixo primeiro:

Assim encontramos:

Agora no eixo :

Então encontramos:

Passo 4

Agora, vamos analisar as forças da junta . Reparando que as barras são perpendiculares, a gente pode fazer o somatório de forças nos eixos desenhados pelas barras. Vamos chamar o eixo CE de e o FD de .

O somatório nos eixos deve zerar:

Assim encontramos:

Agora no eixo :

Então encontramos:

Nesse caso, estando sob compressão.

Passo 5

E vamos também analisar as forças da junta . Vamos chamar FD de e o eixo perpendicular a ele de .

No eixo primeiro:

Assim encontramos:

Agora no eixo :

Então encontramos:

Nesse caso, estando sob tração.

Passo 6

Agora, vamos analisar as forças da junta . Sabendo que o somatório das forças no eixo e somatório das forças do eixo é , pois a estrutura encontra-se em equilíbrio.