Determine a força em cada membro da treliça espacial e indique se os membros estão sob tração ou compressão. A treliça é sustentada por juntas esféricas em , e . Considere . Dica: A reação de apoio em atua ao longo do membro . Por quê?
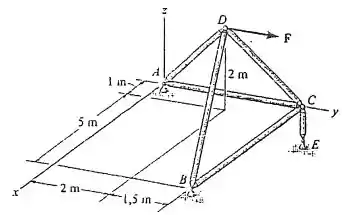
Passo 1
Para determinar as forças, deve-se fazer o diagrama de corpo livre de cada junta no qual sejam indicadas todas as forças atuando no respectivo membro.
Para esse caso é possível fazer apenas a análise das juntas e pelo fato de que elas possuem três forças agindo sobre cada uma e pela possibilidade de encontrar três equações em cada eixo coordenado (, e ), compondo um sistema de equações possível de ser solucionado.
Passo 2
Então, escolhendo a junta primeiro e fazendo o seu DCL, tem-se que:
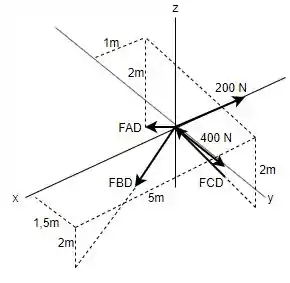
Com isso, é possível montar as equações do equilíbrio de forças para cada eixo.
Então, para o eixo será feito:
Em seguida, para o eixo :
E, em relação ao eixo :
Passo 3
Com as equações , e é possível montar o primeiro sistema de equações cujas soluções serão os valores das forças que agem sobre a junta .
Logo, resolvendo o sistema, obtém-se:
As forças e agem sobre o seu respectivo membro e, portanto, tem caráter trativo. Já a força possui atuação sobre a própria junta e, logo, possui caráter compressivo.
Passo 4
Agora, fazendo o mesmo processo para a junta :
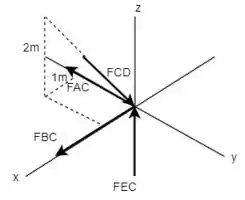
Então, fazendo o equilíbrio de forças:
As forças e agem nos membros da treliça e, por isso, possuem caráter trativo.
A força está agindo sobre o pino, então, possui caráter compressivo.
Resposta
Junta : , e
Junta : , e