Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas fundamentais - Ex. 2
Determine a força em cada membro da treliça. Indique se os membros estão sob tração ou compressão.
Passo 1
Falai galerinha, tudo certo:
Como diria a Viúva Negra, “Ainda somos amigos, certo?”
Boraaa fazer essa comigo
Então já vamos começar com o nosso diagrama de corpo livre da treliça
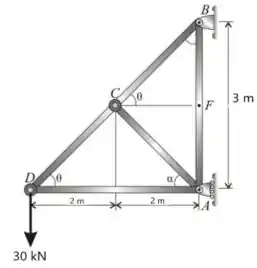
Passo 2
Partindo da geometria da treliça, iremos considerar as seguintes relações.
Calculando o ângulo , temos
Passo 3
Agora iremos calcular o comprimento BF
O ângulo
Passo 4
Vamos desenhar as forças que atuam em diferentes juntas
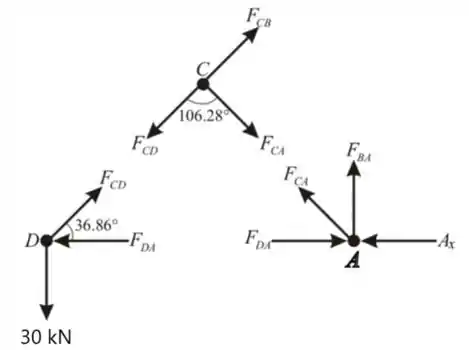
Passo 5
Considerando o método de juntas parar cada uma das juntas C, D, A respectivamente e iremos aplicar a equação de equilíbrio estático, show de bola??
Vamos então considerar a junta D.
Passo 6
Vamos escrever o equilíbrio de forças ao longo da direção horizontal
Escrevendo a equação de equilíbrio de forças ao longo da direção y, teremos
Passo 7
Resolvendo as expressões seguinte, teremos
Passo 8
Vamos considerar agora a junta C
Vamos considerar o equilíbrio de forças ao longo da direção DBC
Considerando o equilíbrio de forças ao longo da direção CA
Substituindo na expressão que encontramos, temos
Passo 9
Agora para finalizarmos, iremos considerar a junta A
Onde, a reação do rolo é representada em corpo livre no pino A
Escrevendo o equilíbrio de forças ao longo da direção horizontal, temos
Agora iremos escrever o equilíbrio de forças ao longo da direção vertical
“Nós somos Groot”
