Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 121
Determine a força no cilindro devida ao peso combinado da caçamba e do operador. A massa combinada é de 180 kg, com centro de massa em .
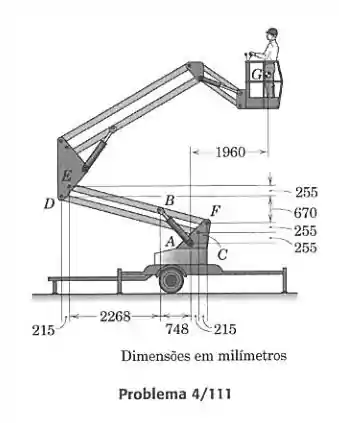
Passo 1
Vamos escolher como nossos corpos a parte que vai da caçamba até o ponto e a barra . Iremos calcular através do momento em torno de para a barra , mas para isso precisamos das forças no ponto . Encontraremos as forças em através das equações de equilíbrio para o primeiro corpo:
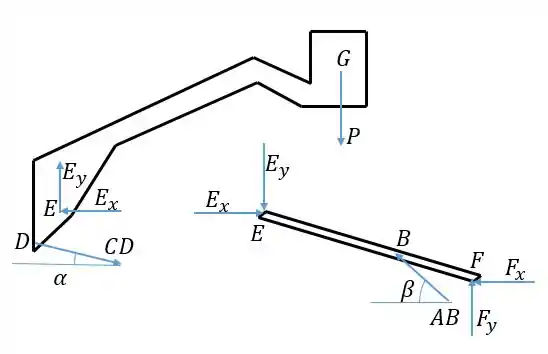
Passo 2
Vamos primeiro encontrar os ângulos e que e fazem com a horizontal, prestando bastante atenção às distâncias que o enunciado dá, conseguimos obter através das tangentes:
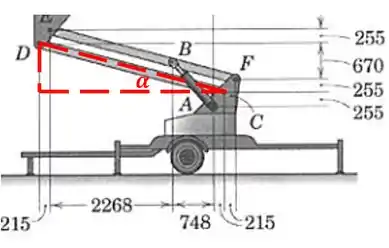
O enunciado não nos dá a distância vertical entre e , mas podemos calculá-la. De até temos 510 mm. A angulação de é de 15.03° como a de , e temos a distância horizontal de a igual a mm:
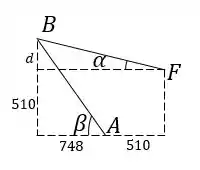
Então achamos a distância :
Então:
Passo 3
Agora que já temos os ângulos, vamos às equações. Primeiro temos o momento em torno de que nos dará . As distâncias vertical e horizontal de a são 255 mm e 215 mm, respectivamente. A distância horizontal de até é:
Calculamos o seno e o cosseno e substituímos pala massa vezes a aceleração da gravidade:
Agora através das somas das forças em e encontramos e :
Passo 4
Vamos então para a barra . Fazendo o momento em torno de , encontramos diretamente a força causada por . A distância horizontal de até é:
E a distância vertical:
E a distância horizontal de a é: