Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 114
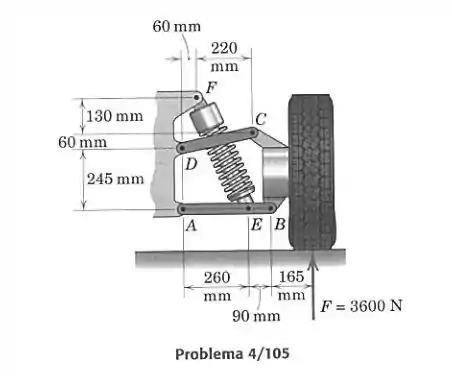
Os elementos da suspensão traseira de um carro com tração dianteira estão mostrados na figura. Determine o módulo da força em cada junta, se a força normal exercida sobre o pneu tem um módulo de 3600N.
Passo 1
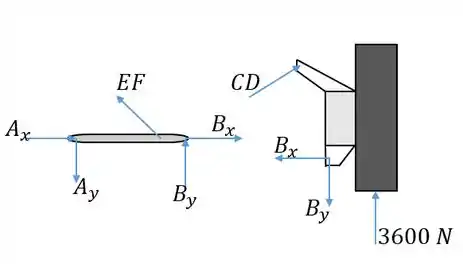
Vamos isolar os corpos mostrados em diagramas de corpo livre, indicando as forças atuantes sobre eles. Devemos tomar cuidado para representar pares ação-reação com sentido contrário. Não precisamos representar e pois são elementos de duas forças.
Passo 2
Para a roda, calculamos diretamente através do momento em relação a . Precisamos primeiro do ângulo que faz com a horizontal. Esse ângulo é dado pela sua tangente:
Então:
Então:
Passo 3
Agora através das somas das forças horizontais e verticais para a roda achamos e :
Fazemos o módulo para achar :
Passo 4
Falta acharmos , e . Para a conexão , calculamos pelo momento em torno de . Calculamos primeiro o ângulo que faz com a horizontal:
Então:
O sinal negativo indica que é de compressão e não de tração como desenhamos. Temos então:
Passo 5
Agora só falta calcular as componentes de , fazendo a soma das forças em e para a conexão :
Basta calcularmos o módulo de :