Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 14

10- Determine a distância z - desde o vértice do cone circular até o centroide de seu volume.

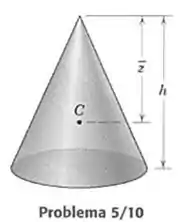
Passo 1

A melhor forma de representar o cone acima é se planificarmos ele de modo a termos o triângulo mostrado abaixo:

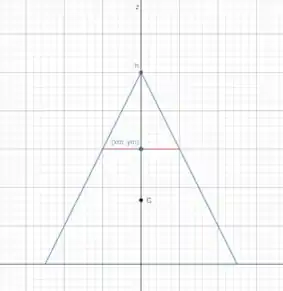
Só que invés de calcular o comprimento dessa linha ( como era no caso do centro de área) agora vamos ter que calcular o tamanho da área que esse disco forma:

Considerando o disco de raio x e altura d z representado pela linha vermelha na figura acima nós temos o elemento de volume dado por:

d V = π x 2   d z

Chamando o raio do círculo da base de r nós teremos a relação.

z - x = h r

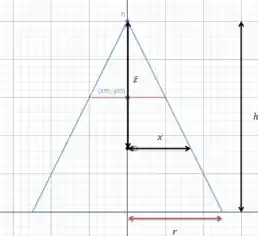
Logo:

x = r z - h

Passo 2

O que faz com que nosso volume seja:

d V = π r 2 h 2   ∫ 0 h z 2   d z = π r 2 h 2 z 3 3 0 h = π r 2 h 3

Que é o volume normal do cone, isso diz que estamos no caminha certo

Passo 3

Assim como para centro de área, o centro de volume não é diferente se estou querendo o tamanho de z - estou analisando discos perpendiculares ao eixo de interesse logo o z médio será o próprio tamanho de z .

z - = ∫ z d V V

Calculando ∫ z   d V :

∫ z   d V = π r 2 h 2 ∫ 0 h z 3 d z = π r 2 h 2 z 4 4 0 h = π r 2 h 2 4

Logo:

z - = π r 2 h 2 4 π r 2 h 3 = 3 h 4

Resposta

z - = 3 h 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centroide y - do sólido homogêneo formado girando-se a área sombreada em torno do eixo y .
Localize o centroide z - do frustum sólido homogêneo do paraboloide formada girando-se a área sombreada em torno do eixo z .
Determine a massa e a localização do centro de massa y - do hemisfério formado girando-se a área sombreada em torno do eixo y . A densidade em qualquer ponto no hemisfério pode ser definida por ρ = ρ
Se a densidade em qualquer ponto na placa retangular é definida por ρ = ρ 0 1 + x a , onde ρ 0 é uma constante, determine a massa e localize o centro de massa x - da placa. A placa tem uma espessura t
Localize o centroide y - do sólido homogêneo formado girando-se a área sombreada em torno do eixo y .