Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 82
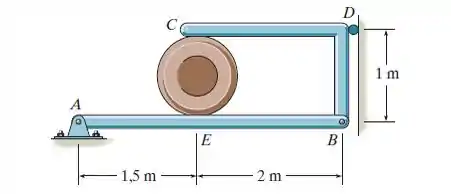
Determine a força que o cilindro liso de 20 kg exerce sobre os membros e . Além disso, quais são as componentes horizontal e vertical da reação do pino
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão que precisamos trabalhar com vários diagramas de corpo livre. Aqui precisamos determinar as reações normais do cilindro sobre os membros e . Além disto, precisamos determinar as reações no pino .
Sendo assim, vamos ter de trabalhar com três diagramas distintos. Vamos fazer o diagrama da estrutura completa, do membro e apenas do cilindro.
Só devemos tomar muito cuidado ao colocarmos forças que aparecem em dois componentes! Pela lei de ação e reação, elas terão um sentido oposto!
Sendo assim, começando os diagramas pela estrutura completa, temos:
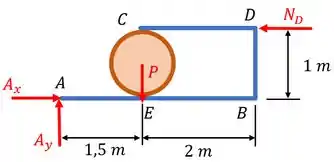
Já para o membro , temos:
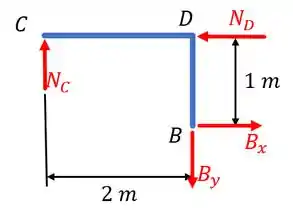
Por fim, para o cilindro, temos:
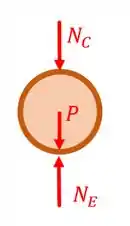
Agora que já temos todas as informações necessárias, vamos as contas!
Passo 2
Vamos começar trabalhando com a estrutura inteira. Aqui nós conseguiremos determinar as reações no apoio em (mas precisamos determinar também!!!).
Para determinarmos as reações nos apoios, temos que utilizar as relações de equilíbrio (somatório de forças e momentos iguais a zero).
Então, utilizando essas relações, temos:
Resolvendo o sistema acima, obtemos:
E assim descobrimos as nossas primeiras reações!
Passo 3
Agora vamos trabalhar com o membro . Conseguem ver o motivo de calcularmos no passo anterior também? Ela é uma forma atuante neste diagrama também!
Bom, continuando, vamos determinar aqui a força que o cilindro exerce em , que é . Para isto, vamos utilizar novamente as equações de equilíbrio. Portanto,
E podemos parar por aqui. Já extraímos as informações necessárias!
Passo 4
Por fim, vamos determinar a reação que o cilindro exerce em . Para isto, temos que analisar o diagrama de corpo livre do cilindro apenas.
Fazendo o somatório de forças na direção vertical, temos:
E assim finalizamos a questão!