Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas de Revisão - Ex. 1
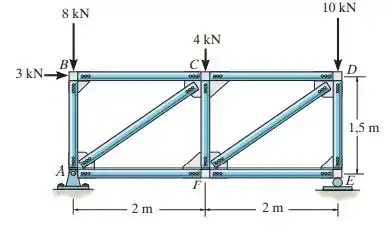
Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão.
Passo 1
Fala, galera. Beleza? Bora para mais um exercício de Mecânica. Para determinarmos a força em cada braço da treliça, vamos primeiro esboçar o DCL:
Agora, que representamos as reações de apoio, vamos determiná-las através das equações de equilíbrio. Temos que a resultante das forças no eixo vai ser:
E para , temos:
Para o momento, temos:
Logo:
Passo 2
Com isso, podemos determinar a força de cada braço da treliça e concluir se eles estão em tração ou compressão. Para isso, vamos utilizar o método dos nós.
Vamos começar pelo nó pois temos menos variáveis que o nó . Logo, vamos esboçar os esforços neste nó:
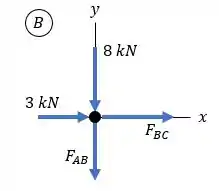
Com isso, vamos utilizar as equações de equilíbrio:
E também:
Passo 3
Agora que a gente conseguiu diminuir o número de incógnitas, já podemos calcular os esforços no nó . Pelo DCL, temos:
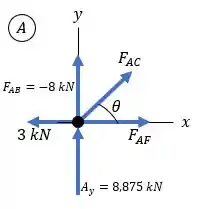
Desta vez, antes de utilizarmos as equações de equilíbrio, precisamos decompor a força . Para isso, precisamos encontrar o ângulo entre esta força e o eixo . Sabemos que:
Pelas equações de equilíbrio, temos:
E também:
Passo 4
Vamos seguir determinando os esforços através dos nós, o processo vai ser o mesmo. Primeiro, para o nó , vamos esboçar os esforços neste nó:
Com isso, vamos utilizar as equações de equilíbrio:
E também:
Passo 5
Em seguida, vamos calcular os esforços no nó . Pelo DCL, temos:
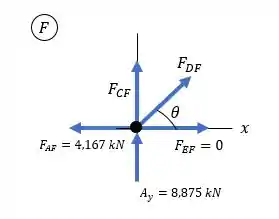
Por semelhança de triângulos, temos que o ângulo vai ser o mesmo:
Pelas equações de equilíbrio, temos:
E também:
Passo 6
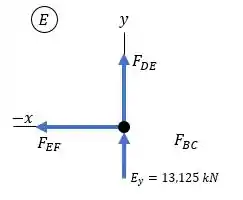
Por fim, vamos determinar os esforços a partir do nó . Temos por semelhança de triângulos que:
Com isso, vamos utilizar as equações de equilíbrio:
Opa, é isso, galera. Bora praticar mais!!!