Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 76
Determine a força (magnitude e direção) que o membro exerce no membro se a carga for aplicada ao centro do membro , e se a carga for aplicada ao centro do membro .
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar o módulo e a direção da força que a barra exerce na barra em duas situações: quando a carga de está aplicada no centro de e quando ela está sendo aplicada no centro de .
Show, então bora lá! Antes de resolver, vamos fazer o diagrama de corpo livre para entendermos melhor o problema.
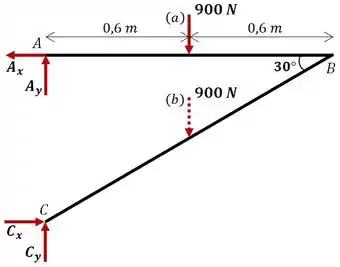
Passo 2
Show! Começando então pelo item . Para resolvê-lo, vamos começar analisando a barra separadamente.
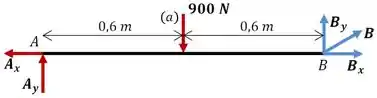
Como a estrutura está em equilíbrio, as barras isoladas também devem estar. Então podemos usar o somatório de momentos em torno de para determinar :
Observe que nós escolhemos calcular o momento em torno do apoio porque isso elimina a necessidade de calcular as reações neste ponto, que não são nosso foco aqui.
Passo 3
Tranquilinho né? Agora para determinar vamos lembrar que é um elemento de duas forças, então a linha de ação da resultante passa pela barra , ou seja, a direção de tem a mesma inclinação de . Logo:
E o módulo de :
Que pode ser escrito vetorialmente como:
Passo 4
Beleza, metade já foi! Agora partiu fazer a segunda parte.
Para resolver a situação , vamos começar calculando a reação vertical em . Como a estrutura está em equilíbrio, podemos usar o somatório de momentos em torno de considerando todas as forças externas atuantes:
Agora podemos isolar a barra , como no item anterior, para encontrar a reação horizontal em :
Novamente, como a estrutura está em equilíbrio, as barras isoladas também devem estar. Então podemos usar o somatório de forças na direção para determinar :
Passo 5
Tá quase acabando hein?! Não desiste não!! Hahaha
Finalmente, podemos isolar a barra . Vamos começar supondo que tenha apenas a componente que calculamos no item anterior. Se essa situação satisfizer a condição de equilíbrio da barra, significa que, de fato, tem apenas componente horizontal.
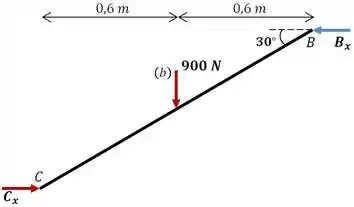
Utilizando então a condição de equilíbrio de momentos em torno de :
Assim confirmamos nossa hipótese de que a força em possui apenas componente vertical e:
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 