Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 71
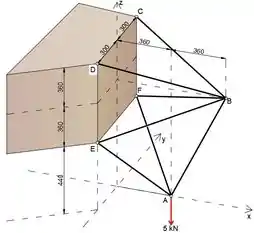
A seção de treliça piramidal BCDEF é simétrica em relação ao plano vertical x-z, como mostrado. Os cabos AE, AF e AB suportam uma carga de 5 kN. Determine a força no membro BE.
Passo 1
Uma vez que a treliça e o carregamento são simétricos ao plano xOz, as forças nos membros AE e AF são iguais, bem como as forças nos membros BE (BD) e BF (BC)
Podemos escrever o vetor de força AE como um produto de sua magnitude AE e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos A e E são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Passo 2
Podemos escrever o vetor de força AF como um produto de sua magnitude AF e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos A e F são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Passo 3
Podemos escrever o vetor de força AB como um produto de sua magnitude AB e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos A e B são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Passo 4
Podemos notar que a força de 5 kN é paralela ao eixo z, portanto, podemos escrevê-la como
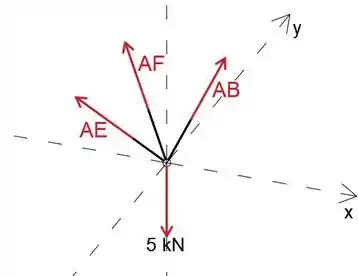
Ao analisar a junta A, podemos determinar o membro de força AB
Presumimos que todos os membros estão em tensão
Agora temos 3 equações de equilíbrio
(1)
(2)
(3)
Passo 5
Uma vez que as forças AE e AF são iguais, podemos escrever a equação (1) como
(1)
Podemos expressar as forças AE e AF em função de AB
Agora podemos substituir AE e AF por 0,366AB na equação (3), a fim de determinar a força no membro AB
Agora podemos escrever o vetor como
Observe que o vetor (BA) ⃗ é oposto ao vetor AB ⃗, então podemos escrevê-lo como
Ao analisar a junta B e usando simetria, podemos determinar a força no membro BE
Mais uma vez, assumimos que todos os membros estão em tensão
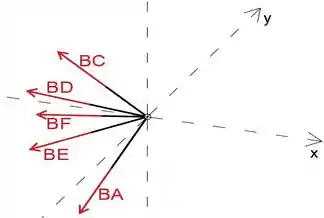
Passo 6
Podemos escrever o vetor de força BC como um produto de sua magnitude BC e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos A e B são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Passo 7
Podemos escrever o vetor de força BD como um produto de sua magnitude BD e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos B e D são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Passo 8
Podemos escrever o vetor de força BF como um produto de sua magnitude BF e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos B e F são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Passo 9
Agora que escrevemos todas as forças como vetores, podemos escrever três equações de equilíbrio igualando a soma das forças a zero
Agora temos 3 equações de equilíbrio
(4)
(5)
(6)
Passo 10
Uma vez que sabemos por simetria que as forças BC e BD são iguais, bem como as forças BE e BF, podemos escrever a equação (4) como
Multiplicando por , temos
Também podemos escrever a equação 6 como
Finalmente, adicionando as equações (7) e (8), podemos determinar a força BE
uma vez que obtivemos resultado negativo, isso significa que o membro BE está em compressão