Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 105
Determine a força P que deve ser aplicada em A para sustentar a caixa de 100 kg. Existem dois de cada membro mostrado com membros de conexão (perpendiculares ao papel) em cada junta, e uma plataforma leve liga os dois membros DE. O atrito nas juntas é insignificante e todos os membros são leves. O atrito sob os membros CF é suficiente para evitar o deslizamento.
Passo 1
E ai galera tudo certinho° Primeiro, isole bem e desenhe o diagrama de corpo livre da plataforma de luz.
O peso da caixa é
Observe que há dois membros de cada membro atuando na plataforma.
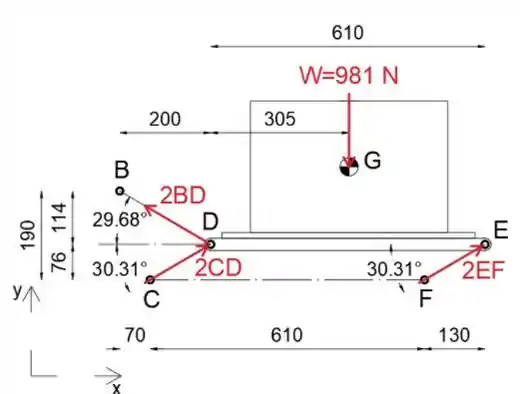
O ângulo que os membros CD e EF fazem com a horizontal é:
O ângulo que o membro BD faz com a horizontal é:
Passo 2
Ao igualar a soma dos momentos sobre o ponto A a zero, podemos determinar a força EF
Ao igualar a soma das forças na direção x a zero, escreveremos o CD de força como função de BD.
A partir daqui, podemos expressar o CD como:
Equacionando a soma das forças na direção y a zero, podemos determinar a força BC
Substitua pela expressão (1)
Passo 3
Equacionando a soma dos momentos sobre o ponto C a zero, podemos determinar a força P
A partir daqui, podemos expressar a força P como:
Substitua por seu valor.