Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 93
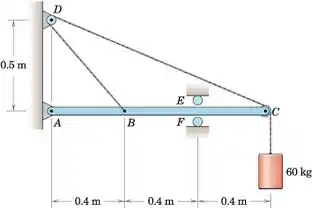
Determine a magnitude da reação do pino em A e a magnitude e a direção da reação da força nos rolos. As polias em C e D são pequenas.
Passo 1
Quando olhamos para o nosso sistema, podemos notar que existem dois rolos nos pontos E e F que podem suportar a única compressão e, uma vez que estão posicionados em lados opostos da barra AC, isso significa que apenas um dos dois rolos estará em uso
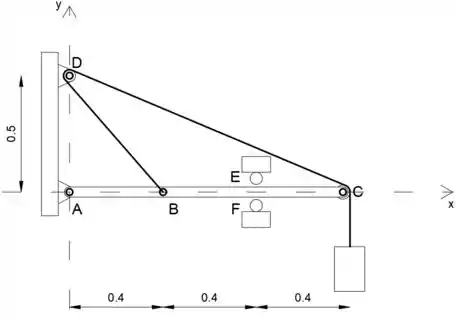
Portanto, podemos substituir os rolos em E e F por um suporte de rolo em F, que pode suportar tanto a tensão quanto a compressão
Passo 2
Observe que se a reação em F é compressão, isso significa que originalmente o suporte F está em uso, enquanto a força de reação em E será zero, ou seja, se a reação em F for tensão, isso significa que originalmente o suporte E está em uso, enquanto a força de reação em F será zero
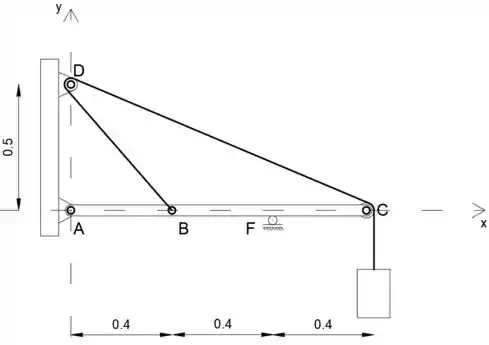
Como sabemos que a tensão no cabo é igual ao peso da carga de 60 kg, podemos isolar o membro AC com as forças de reação em A e F e as forças de tensão em B e C atuando nele
Observe que os ângulos machos BD e CD e com eixo z respectivamente
Passo 3
Vamos supor que o apoiador F está em compressão
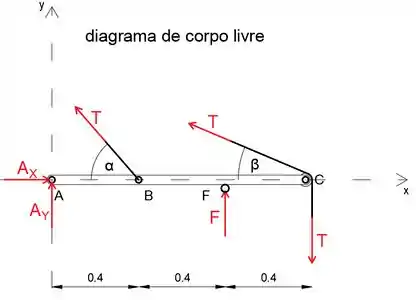
Equacionando a soma dos momentos sobre o ponto A, eliminaremos as forças de reação em A, para que possamos determinar a força F
Passo 4
Uma vez que a reação em F é a compressão, isso significa que a força de reação do rolo E é igual a zero
Equacionando a soma das forças na direção x e y a zero, determinaremos as forças de reação em A
Finalmente, usando o teorema de Pitágoras, podemos calcular a magnitude da força de reação em A