Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 95
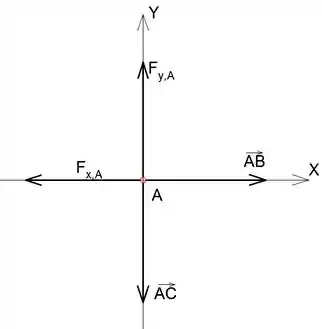
Determine a força de corte F aplicada pela lâmina DE à barra em G em termos da força P aplicada ao cabo do cortador de alta resistência. Suponha que a força de corte F é perpendicular à borda inferior da lâmina DE.
Passo 1
Neste exercício, devemos calcular as forças no membro , , . Para o primeiro, devemos calcular as reações externas na junção A e C. Na junção C, devido ao tipo de suporte, temos apenas uma reação, que é horizontal. Na junta A, existem 2 reações externas, horizontais e verticais. Antes de escrevermos a equação de equilíbrio, vamos converter a unidade de massa em unidade de peso.
Vamos escrever equações de equilíbrio para uma determinada treliça carregada:
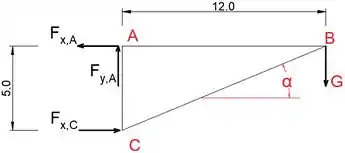
Passo 2
Agora, quando temos reações externas, podemos escrever equações de equilíbrio para as articulações. Vamos escrever equações de equilíbrio para a junta C, mas primeiro devemos calcular o ângulo entre a horizontal e a barra BC.
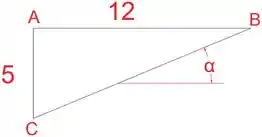
Agora, podemos escrever equações de equilíbrio para a junta B:
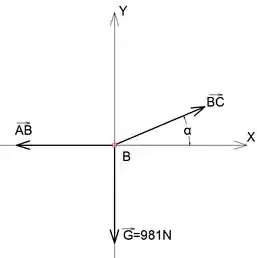
Passo 3
Agora, sabemos 2 membros (AB e BC) e apenas o membro desconhecido é AC. Podemos calcular esse membro a partir de equações de equilíbrio para a junta A ou C, da mesma forma. Vamos escrever equações de equilíbrio para a junta A:
