Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 17
Determine a força no elemento DE e em cada um dos elementos localizados à esquerda de DE para a treliça de telhado tipo Howe invertida mostrada na figura. Indique se cada elemento está sob tração ou sob compressão.
Passo 1
Vamos começar o exercício desenhando o diagrama de corpo livre da treliça:
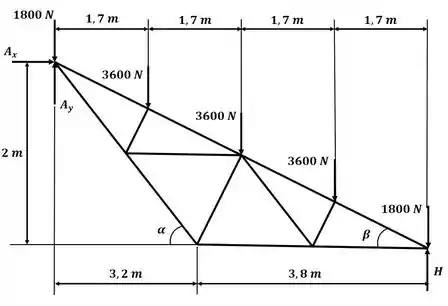
Agora aplicando o somatório de forças na direção :
Agora aplicando o somatório de momento com relação ao ponto H, temos:
E, aplicando o somatório de forças na direção :
Antes de começarmos a analisar os nós, vamos encontrar os ângulos e do diagrama que serão usados para decompor as forças nos nós, então:
Passo 2
Agora vamos analisar o nó A:
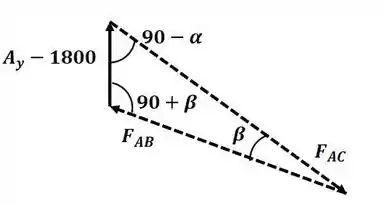
Aplicando a lei dos senos para o triângulo de forças e substituindo os valores encontrados no passo 1, temos:
Pegando a primeira e terceira parcela, temos:
Pegando a segunda e terceira parcela, temos:
Agora vamos analisar o nó B:
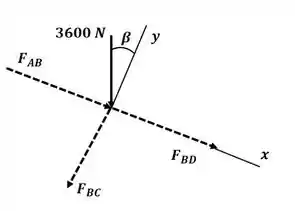
Aplicando o somatório de forças na direção :
Agora aplicando o somatório de forças na direção :
Passo 3
Agora vamos analisar o nó C:
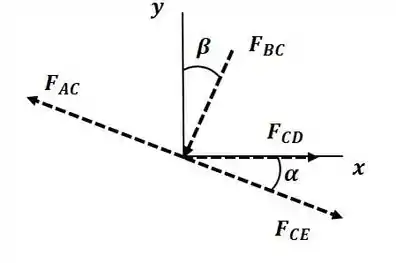
Aplicando o somatório de forças na direção :
Agora aplicando o somatório de forças na direção :
Agora vamos analisar o nó E:
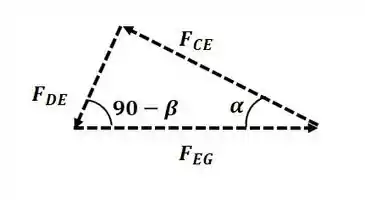
Aplicando a lei dos senos para o triângulo de forças e substituindo os valores encontrados no passo 1, temos: