Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 61
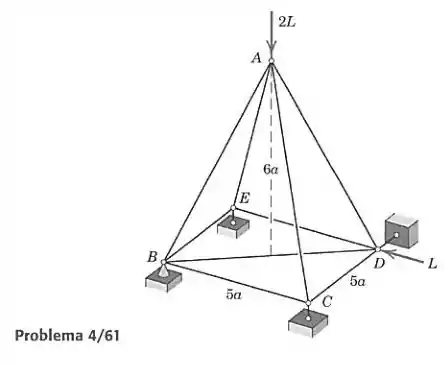
Determine a força no elemento da prirâmide regular de base quadrada.
Passo 1
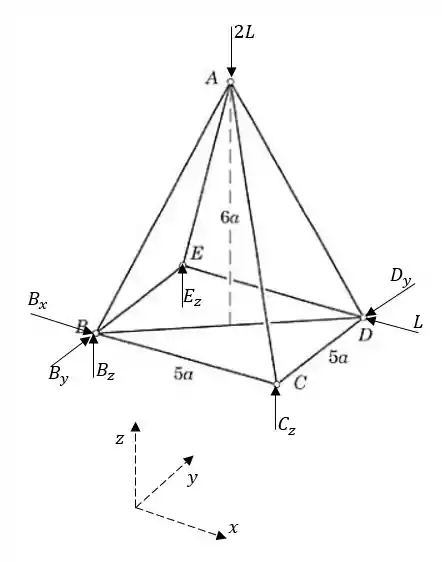
Vamos primeiro analisar as forças externas da pirâmide como um todo e depois disso analisar as condições de equilíbrio para os nós. Fazemos primeiro um desenho das forças externas atuantes na treliça. Temos que prestar atenção nos tipos de fixação. A fixação em pode causar força em todas as direções, as fixações em e apenas na direção e a fixação em apenas na direxão .
Passo 2
Queremos encontrar , e vamos fazer isso através das condições de equilíbrio para o nó . Mas temos nesse ponto 5 forças desconhecidas. Como temos 3 equações de força, devemos ter só 3 incógnitas quando formos olhar para esse ponto. Devemos primeiro então com as equações da treliça toda e de mais algum nó encontrar 2 forças que estão em .
Primeiro vamos fazer o momento em torno de pois há muitas forças nesse eixo e passando por ele. As únicas forças que não apssam por ele ou são paralelas são e a força em , então:
Podemos encontrar fazendo o momento em torno de um eixo na direção passando por . As únicas forças que não passam pelo eixo e não são paralelas são e a força aplicada em :
Já achamos uma força que passa em . Não há mais equações envolvendo poucas forças que sejam úteis para a treliça inteira, então agora vamos tentar achar a outra de outra maneira.
Passo 3
Como achamos , agora só temos 3 incógnitas no ponto e se fizermos as equações para esse nó podemos encontrar que é muito útil para a gente. Devemos colocar as forças na forma de módulo vezes vetor unitário.
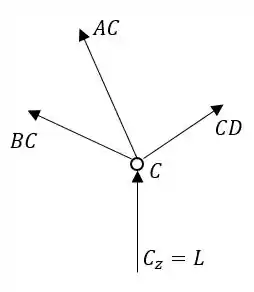
Os vetores de e têm a forma:
Precisamos calcular o vetor unitário de . Temos:
Então:
Como só temos como incógnita na direção , fazemos a soma ser zero nessa direção:
Agora fazendo a soma na direção :
Passo 4
Finalmente temos só 3 incógnitas em ! Agora vamos às equações para esse nó.
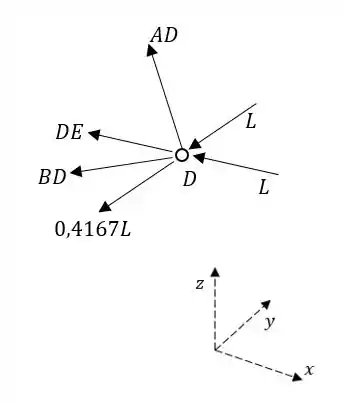
Primeiramente, olhamos que só tem na direção , e como a força em tem que ser zero . Na direção só tem como vetor, então vamos usar a soma das forças em agora. O ângulo que faz com essa direção é de 45°: