Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 225

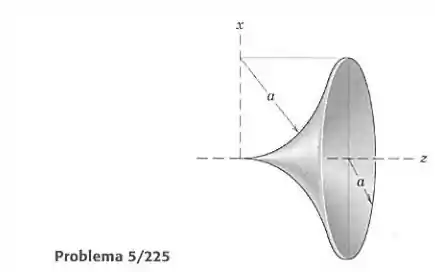
Localize o centro de massa da casca homogênea, em formato de sino, de espessura uniforme, mas desprezível.

Passo 1

Primeiramente, pela simetria em torno do eixo z , vemos que o centro de massa deve estar sobre esse eixo. Devemos então calcular só a coordenada z do CM. Vamos dividir o sino fazendo cortes perpendiculares ao eixo de simetria, formando círculos com centro no eixo, e raios que tem tamanho indo de zero, quando x = 0 até a , quando x = a . A coordenada z do CM será dada por:

z - = ∫ z   d A ∫ d A

Passo 2

Olhando perpendicularmente ao plano x z , vamos centrar um círculo em x = a , z = 0 , com raio a , e variar o ângulo θ em relação ao eixo x de 0 a π 2 , como mostra a figura:

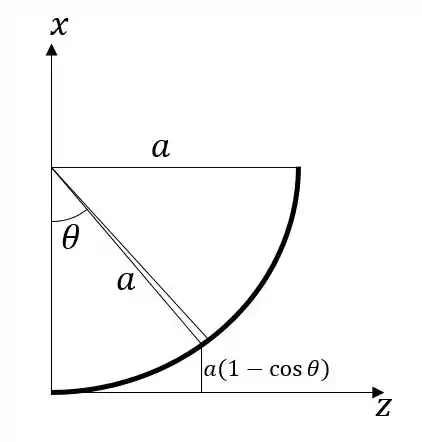
O raio em função de θ do círculo que compõe o sino é a ( 1 - cos ⁡ θ ) . A largura infinitesimal do círculo é d l = a   d θ . Então a área é:

d A = 2 π r   d l = 2 π a 1 - cos ⁡ θ ⋅ a d θ = 2 π a 2 1 - cos ⁡ θ d θ

E a coordenada z é:

z = a sen ⁡ θ

Passo 3

Vamos então calcular a integral ∫ z   d A :

∫ z   d A = ∫ 0 π / 2 a sen ⁡ θ ⋅ 2 π a 2 1 - cos ⁡ θ d θ = 2 π a 3 ∫ 0 π / 2 sen ⁡ θ d θ - ∫ 0 π / 2 sen ⁡ θ cos ⁡ θ d θ

Usamos agora que sen ⁡ θ cos ⁡ θ = sen ⁡ 2 θ 2

∫ z   d A = 2 π a 3 - cos ⁡ θ 0 π / 2 + cos ⁡ 2 θ 4 0 π / 2 = 2 π a 3 - cos ⁡ π 2 + cos ⁡ 0 + cos ⁡ π 4 - cos ⁡ 0 4

= 2 π a 3 1 - 1 4 - 1 4 = 2 π a 3 1 2 = π a 3

Passo 4

Agora vamos calcular a massa da casca ∫ d A .

∫ d A = ∫ 0 π / 2 2 π a 2 1 - cos ⁡ θ d θ = 2 π a 2 θ - sen ⁡ θ 0 π / 2

= 2 π a 2 π 2 - 0 - sen ⁡ π 2 + sen ⁡ 0 = 2 π a 2 π 2 - 1 = π ( π - 2 ) a 2

Passo 5

Finalmente, dividimos as duas integrais para obter z - :

z - = ∫ z   d A ∫ d A = π a 3 π π - 2 a 2 = a π - 2

Resposta

x - = y - = 0

z - = a π - 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O planador A está sendo rebocado em vôo nivelado e está a 400 pés atrás e 100 pés abaixo do plano de reboque B. A tangente ao cabo do planador é horizontal. O cabo pesa 0,5 lb por pé de comprimento. C
A viga I suporta a força de 1000 lb e o par de 2000 lb-ft aplicado ao suporte de 2 pés soldado na extremidade da viga. Calcule o cisalhamento V e o momento M na seção intermediária entre A e B.
O cabo de massa desprezível é suspenso nos dois pontos fixos mostrados, e a tensão no suporte inferior é suficiente para manter a inclinação zero do cabo naquele ponto. O cabo suporta uma carga unitár
Uma luminária está suspensa no teto de um pórtico externo. Quatro correntes, duas das quais são mostradas, evitam o movimento excessivo do aparelho durante condições de vento. Se as correntes pesarem
O cabo de luz tem inclinação zero em seu ponto inferior de fixação e suporta a carga unitária que varia linearmente com x de w0 a w1 conforme mostrado. Derive a expressão para a tensão no cabo na orig