Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 31
Determine a força nos membros , e da treliça e indique se os membros estão sob tração ou compressão.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
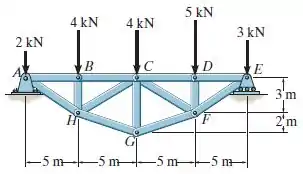
Temos aqui um problema em que precisamos determinar a força nos membros , e da treliça e indicar se a mesma é de tração ou de compressão.
Além disto, a questão pede para esboçarmos o diagrama de corpo livre, o que é exatamente a primeira coisa que faremos. Portanto, substituindo os apoios pelas suas reações, temos:
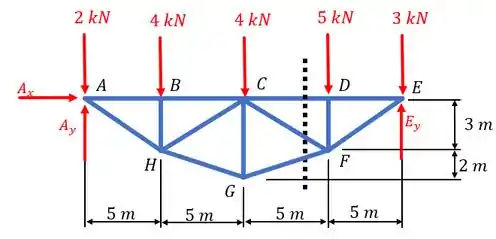
Vamos aproveitar o momento para calcularmos a reação . Ela será necessária para determinarmos as reações nos membros , e , como poderemos ver no Passo 2.
Então, para determinarmos , basta realizarmos o somatório dos momentos em torno do ponto , pois assim eliminaremos as suas reações da equação. Logo,
E assim podemos dar continuidade a questão!
Passo 2
Para podermos determina as forças nos membros , e teremos que fazer utilizar o método das seções. Para isto, no diagrama de corpo livre do Passo 1, nós indicamos aonde deve ser realizado o corte por uma linha preta tracejada.
Realizando este corte, teremos o seguinte diagrama:
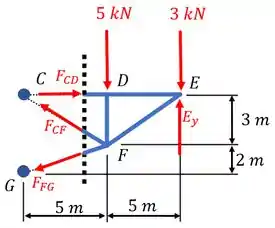
Agora, basta aplicarmos uma das equações de equilíbrio para determinarmos cada uma das forças. Portanto, começando pelo somatório de momentos em torno de , temos:
Apesar da força não ser pedida na questão, ela será importante para continuarmos com os cálculos. Portanto, para o somatório dos momentos em torno de , temos:
E para finalizarmos a análise do método das seções, temos de calcular . Para isto, vamos fazer o somatório de forças na direção . Portanto,
Passo 3
Para finalizarmos a questão, devemos obter a força . Para isto, ao invés de utilizarmos o método das seções, vamos utilizar os métodos dos nós.
Escolhendo o nó , teremos o seguinte diagrama de equilíbrio:
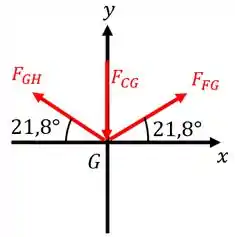
Aplicando as equações do equilíbrio, obtemos:
E assim finalizamos a questão!