Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 44
Determine a força nos membros , , e da treliça e indique se os membros estão sob tração ou compressão.
Passo 1
Oi, tudo bem? Vamos analisar esta questão.
Para trabalhar com analise de treliças é aconselhável seguir um passo a passo para deixar os cálculos mais organizados e para não confundir os elementos.
Primeiro devemos construir um diagrama de corpo livre e descobrir o valor das reações de apoio externas. Temos que:
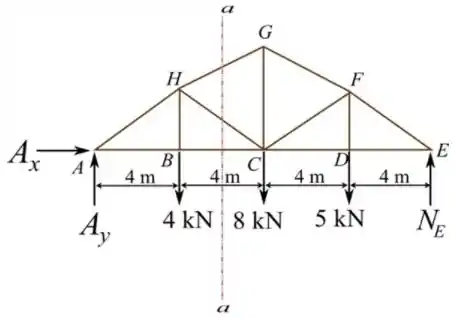
Fazendo o somatório de momento em , temos que:
Resolvendo, temos que:
Do somatório de forças em , temos que:
Passo 2
O segundo passo é a análise interna dos elementos. Queremos a força nos membros , , e . Observe o diagrama:
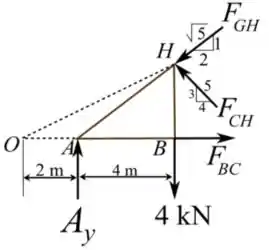
Podemos fazer primeiro o somatório de momentos em , pois eliminaríamos da equação as forças que passam diretamente no ponto . Temos que:
Como já descobrimos que , temos que:
Como o valor calculado ficou positivo, significa que acertamos a direção da força no nosso desenho e, portanto, trata-se de uma tração.
Passo 3
Agora, vamos aplicar o somatório de momentos em . Temos que:
Já temos o valor de , portanto:
Como o valor calculado ficou positivo, significa que acertamos a direção da força no nosso desenho e, portanto, trata-se de uma compressão.
Se fizermos o somatório de momentos em , teremos:
Logo:
Como o valor calculado ficou positivo, significa que acertamos a direção da força no nosso desenho e, portanto, trata-se de uma compressão.
Passo 4
Ainda precisamos descobrir a reação interna no elo .
Para isso, vamos considerar o ponto , como nosso ponto de estudo agora. Temos que:
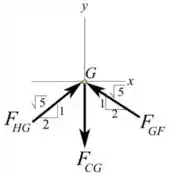
Analisando as forças em , temos que:
Analisando em , temos que:
Como o valor calculado ficou positivo, significa que acertamos a direção da força no nosso desenho e, portanto, trata-se de uma tração.