Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 31
Determine a força no elemento da treliça carregada.
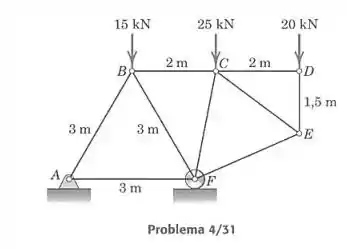
Passo 1
Vamos calcular as forças pelo método das seções. Traçamos uma seção passando por , e , tratando a parte da direita como se fosse um só corpo rígido. O nosso desenho então fica assim:
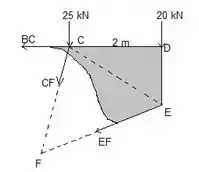
Devemos resolver as equações de equilíbrio pra esse corpo pra encontrarmos a força de .
Passo 2
Podemos ver no desenho que temos 2 forças desconhecidas passando por F. Então se calcularmos o momento em torno de F essas duas não aparecerão na equação, e então poderemos achar diretamente.
Mas pra isso, primeiro precisamos calcular algumas distâncias no nosso desenho.
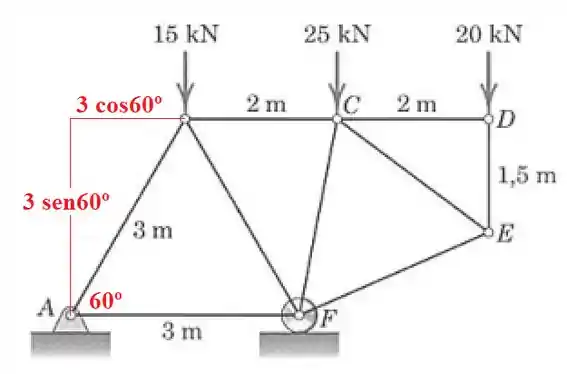
Então, considerando uma força BC pra esquerda, o somatório de momentos fica:
Como o valor deu positivo, a barra está tracionada como chutamos no desenho.
Resposta
Exercícios de Livros Relacionados
6.34. Determine a força nos membros JK, CJ e CD da treliça e indique se os membros estão sob tração ou compressão.
6.33. A treliça de ponte Howe está sujeita ao carregamento mostrado. Determine as forças nos membros HI, HB e BC e indique se os membros estão sob tração ou compressão.
6.32. A treliça de ponte Howe está sujeita ao carregamento mostrado. Determine as forças nos membros HD, CD e GD e indique se os membros estão sob tração ou compressão.
44. Uma treliça de ponte Warren é carregada tal como mostra a figura. Determine a força nos elementos E G ,F G e F H .
61. Determine a força nos elementos A F e E J da treliça mostrada na figura quando P = 1,2k N e Q = 0 . (Dica: use a seção a a )