Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 231
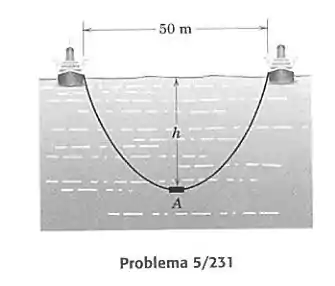
Um instrumento de detecção submarina está preso ao ponto médio de um cabo de 100 m, suspenso entre dois barcos distando 50 m entre si. Determine a profundidade do instrumento, que tem massa desprezível. O resultado depende da massa do cabo ou da massa específica da água?
Passo 1
Para esse problema primeiro devemos perceber que nesse cabo, como estão agindo sobre cada pedaço além da tração a força peso e a força do empuxo, que são funções apenas do comprimento, temos a configuração de um cabo caternário. Esse tipo de cabo tem o formato dado pela seguinte equação:
Escolhendo como origem o ponto mais baixo, temos o ponto pertencendo à curva, então:
Sendo a tração horizontal no ponto mais baixo da corda e a intensidade da força por metro da corda. Outra equação dada pelo livro nos diz que para o cabo catenário o tamanho da corda indo da origem até o ponto de coordenada é dado por:
Então devemos achar o valor de utilizando a eq. (2), e então aplicar a eq. (1) para encontrar o valor de .
Passo 2
Vamos primeiro aplicar a eq. (2) para achar o valor de . Temos:
Não temos ainda o valor de , que é a força que a corda sofre por metro de comprimento, devido ao peso e ao empuxo. Vamos deixar só em função de , pois não sabemos ainda se o resultado irá depender da massa da corda e da densidade da água. Pela simetria, sabemos que o comprimento da corda da origem até a abscissa é metade da corda e igual a 50 m. Então:
Vamos chamar a razão de de . Nossa equação em função de é:
Resolvendo com auxílio de um computador, chegamos ao valor de :
Passo 3
Agora vamos olhar para a eq. (1). Ela dá a coordenada da corda em função de :
Sabemos que a extremidade da direita tem coordenadas , então substituímos:
Mas já calculamos no Passo 2 a razão e então substituímos: