Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 30
Determine a força no elemento da treliça carregada.
Passo 1
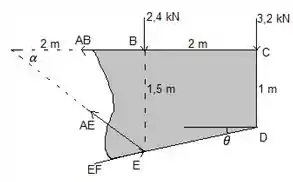
Vamos calcular as forças pelo método das seções. Traçamos uma seção passando por , e , tratando a parte da direita como se fosse um só corpo rígido. O nosso desenho então fica assim:
Passo 2
Agora devemos ser capazes de fazer as equações de equilíbrio para encontrar as forças, pois temos 3 forças desconhecidas e 3 equações de equilíbrio. Devemos primeiro achar os ângulos e . Temos:
Passo 3
Agora vamos às equações de equilíbrio. T significa que o elemento é de tração e
C que é de compressão. Fizemos no desenho chutes se as barras são de tração ou compressão, se obtivermos valor negativo quer dizer que erramos no chute e ela será do outro tipo. Vamos começar com o momento em torno de E, pois não usamos 2 forças desconhecidas nessa equação:
Agora o equilíbrio no eixo :
Substituindo os valores dos cossenos achamos em função de :
Agora o equilíbrio em :
Substituindo os senos e :