Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 59
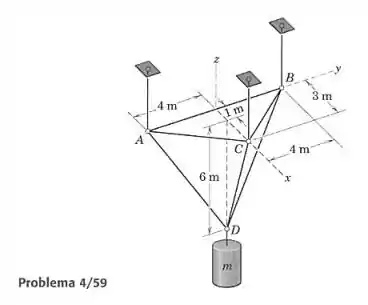
A treliça espacial tetraédrica tem uma base horizontal na forma de um triângulo isósceles e pernas , e que suportam a massa no ponto . Cada vértice da base é suspenso por um cabo vertical preso em suportes superiores. Calcule as forças induzidas nos elementos e .
Passo 1
Vamos calcular as forças pelo método dos nós, aplicando as três equações de equilíbrio (para , e ) no ponto , pois nesse ponto temos as forças que queremos achar. Existem nesse nó como incógnitas as forças nos elementos , , e a força no cabo vertical. Então, como só temos 3 equações, não conseguimos resolver para essas 4 incógnitas. Devemos encontrar antes, de outra maneira, aplicando equações de equilíbrio para a treliça como um todo.
Passo 2
Queremos primeiro fazer as equações de equilíbrio na treliça como um todo pra encontrar as forças verticais em , e . É mais conveniente trabalhar com equações que só tem uma incógnita, então fazer a equação do momento total em torno de é bom, porque e estão no eixo e e não entram na conta. Então:
Agora, pela simetria que há na estrutura em relação ao plano , fica claro que temos:
Então só teremos uma incógnita no cálculo da força total no eixo :
Resolvendo achamos :
Passo 3
Agora já temos , então só sobraram 3 forças desconhecidas em , o que significa que conseguimos resolver o sistema com as 3 equações de equilíbrio. Precisamos das expressões dos vetores unitários de , e para fazermos as equações tendo como incógnita só os módulos. Temos:
é fácil de definir porque ele é o próprio vetor . Então:
Agora para :
Então:
Só falta fazer para :
Passo 4
Agora basta somar os vetores das 4 forças atuantes em e igualar a zero:
Agrupamos os termos em , e :
Cada um dos valores multiplicados pelos vetores unitários tem que ser zero, então temos 3 equações. Vamos primeiro pra última, que só tem uma incógnita:
Agora a primeira:
Substituindo :
O valor negativo significa que a força comprime a barra, e não traciona. Faltou apenas uma equação:
Substituindo os valores já encontrados:
Novamente obtivemos sinal negativo, então a força é de compressão.